如图，在平面直角坐标系 ${xOy}$ 中，直线 ${y}={-x}+{3}$ 与 ${x}$ 轴交于点 ${C}$，与直线 ${AD}$ 交于点 ${A}\left(\dfrac{4}{3},\dfrac{5}{3}\right)$，点 ${D}$ 的坐标为 $\left(0,1\right)$．直线 ${AD}$ 与 ${x}$ 轴交于点 ${B}$，若点 ${E}$ 是直线 ${AD}$ 上一动点（不与点 ${B}$ 重合），当 $\triangle {BOD}$ 与 $\triangle {BCE}$ 相似时，求点 ${E}$ 的坐标．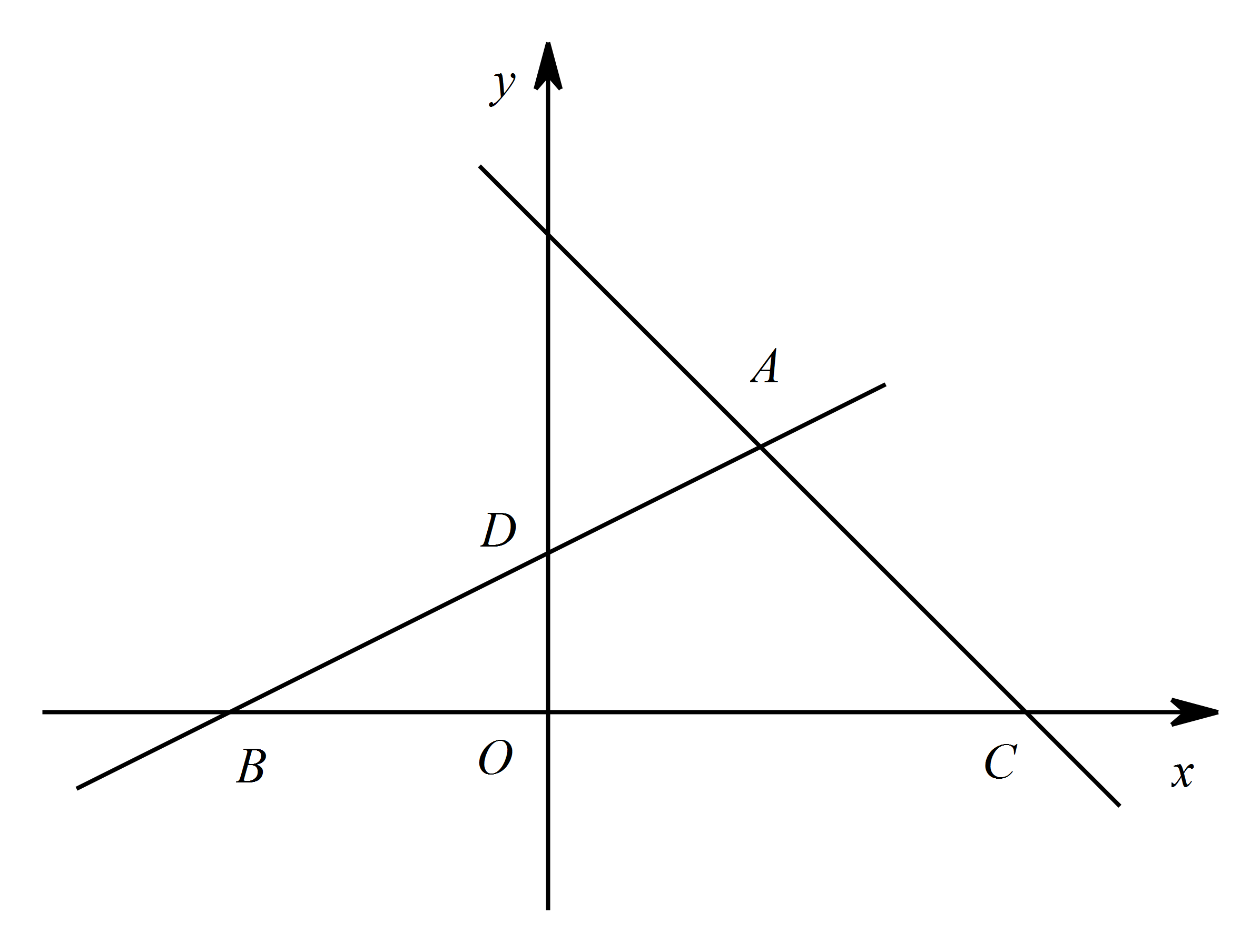
【难度】
【出处】
无
【标注】
【答案】
$\left(3,\dfrac52\right)$，$\left(2,2\right)$
【解析】
设直线 $AD$ 的解析式为 $y=kx+b$，
将点 ${A}\left(\dfrac{4}{3},\dfrac{5}{3}\right)$，点 ${D}\left(0,1\right)$ 代入直线 $y=kx+b$ 中，得
$\begin{cases}\dfrac{4}{3}k+b=\dfrac{5}{3} ,\\ b=1.\end{cases}$
解得 $\begin{cases} k=\dfrac 12,\\ b=1.\end{cases}$
所以直经 $AD$ 的解析式为：$y=\dfrac12x+1$．
设点 $E$ 的坐标为 $\left(m,\dfrac {1}{2}m+1\right)$．
令 $y=\dfrac{1}{2}x+1=0$，得 $x=-2$，
所以点 $B$ 的坐标为 $\left(-2,0\right)$．
令 $y=-x+3=0$，得 $x=3$，
所以点 $C$ 的坐标为 $\left(3,0\right)$，
所以 $OB=2$，$OD=1$，$BC=5$，$BD=\sqrt{1+2^2}=\sqrt5$．
当 $\triangle BOD \backsim \triangle BCE$ 时，如图所示，过点 $C$ 作 $CE \perp BC$ 交直线 $AB$ 于 $E$．
所以 $\dfrac{OB}{BC}=\dfrac{OD}{CE}$，
所以 $\dfrac 25=\dfrac 1{CE}$，
所以 $ CE=\dfrac52$，
所以 $\dfrac{1}{2}m+1=\dfrac52$，解得 $m=3$．
所以 $ E$ 点的坐标为 $\left(3,\dfrac52\right)$．
当 $\triangle BOD \backsim \triangle BEC$ 时，如图所示，过点 $E$ 作 $EF \perp BC$ 于 $F$ 点．
则 $\dfrac{OD}{CE}=\dfrac{BD}{BC}$．
所以 $ \dfrac{1}{CE}=\dfrac{5}{\sqrt5}$，
所以 $ CE=\sqrt5$，
所以 $ BE=\sqrt{{BC}^2-{CE}^2}=\sqrt{25-5}=2\sqrt5$，
所以 $\dfrac{1}{2}BE\cdot CE=\dfrac{1}{2}EF\cdot BC$，
所以 $2\sqrt5\cdot\sqrt5=EF \cdot5$，
所以 $EF=2$，
所以 $ \dfrac{1}{2}m+1=2$，解得 $m=2$．
所以 此时 $E$ 点的坐标为 $\left(2,2\right)$．
当 $\triangle BOD$ 与 $\triangle BCE$ 相似时，满足条件的 $E$ 坐标 $\left(3,\dfrac52\right)$，$\left(2,2\right)$
将点 ${A}\left(\dfrac{4}{3},\dfrac{5}{3}\right)$，点 ${D}\left(0,1\right)$ 代入直线 $y=kx+b$ 中，得
$\begin{cases}\dfrac{4}{3}k+b=\dfrac{5}{3} ,\\ b=1.\end{cases}$
解得 $\begin{cases} k=\dfrac 12,\\ b=1.\end{cases}$
所以直经 $AD$ 的解析式为：$y=\dfrac12x+1$．
设点 $E$ 的坐标为 $\left(m,\dfrac {1}{2}m+1\right)$．
令 $y=\dfrac{1}{2}x+1=0$，得 $x=-2$，
所以点 $B$ 的坐标为 $\left(-2,0\right)$．
令 $y=-x+3=0$，得 $x=3$，
所以点 $C$ 的坐标为 $\left(3,0\right)$，
所以 $OB=2$，$OD=1$，$BC=5$，$BD=\sqrt{1+2^2}=\sqrt5$．
当 $\triangle BOD \backsim \triangle BCE$ 时，如图所示，过点 $C$ 作 $CE \perp BC$ 交直线 $AB$ 于 $E$．
所以 $\dfrac{OB}{BC}=\dfrac{OD}{CE}$，所以 $\dfrac 25=\dfrac 1{CE}$，
所以 $ CE=\dfrac52$，
所以 $\dfrac{1}{2}m+1=\dfrac52$，解得 $m=3$．
所以 $ E$ 点的坐标为 $\left(3,\dfrac52\right)$．
当 $\triangle BOD \backsim \triangle BEC$ 时，如图所示，过点 $E$ 作 $EF \perp BC$ 于 $F$ 点．
则 $\dfrac{OD}{CE}=\dfrac{BD}{BC}$．所以 $ \dfrac{1}{CE}=\dfrac{5}{\sqrt5}$，
所以 $ CE=\sqrt5$，
所以 $ BE=\sqrt{{BC}^2-{CE}^2}=\sqrt{25-5}=2\sqrt5$，
所以 $\dfrac{1}{2}BE\cdot CE=\dfrac{1}{2}EF\cdot BC$，
所以 $2\sqrt5\cdot\sqrt5=EF \cdot5$，
所以 $EF=2$，
所以 $ \dfrac{1}{2}m+1=2$，解得 $m=2$．
所以 此时 $E$ 点的坐标为 $\left(2,2\right)$．
当 $\triangle BOD$ 与 $\triangle BCE$ 相似时，满足条件的 $E$ 坐标 $\left(3,\dfrac52\right)$，$\left(2,2\right)$
答案
解析
备注
