如图,抛物线 $y=x^2$ 的顶点为 $O$,$AB$ 是过焦点 $F$ 的一条长度为 $2$ 的弦,$D$ 是 $AB$ 的中垂线与 $y$ 轴的交点.求四边形 $AOBD$ 的面积.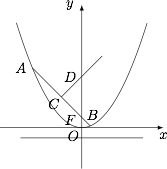

【难度】
【出处】
2012年全国高中数学联赛江西省预赛
【标注】
【答案】
$\dfrac{5\sqrt2}{8}$
【解析】
设点 $A,B$ 的坐标分别为 $A(x_1,y_1),B(x_2,y_2)$.
由条件知,抛物线的焦点为 $F\left(0,\dfrac14\right)$,准线方程为 $y=-\dfrac14$.
根据抛物线定义得,$$AF=y_1+\dfrac14,BF=y_2+\dfrac14,$$所以$$2=AF+BF=y_1+y_2+\dfrac12,y_1+y_2=\dfrac32.$$$AB$ 的中点为 $C\left(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2}\right)$,又因为$$k_{AB}=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{x_2^2-x_1^2}{x_2-x_1}=x_1+x_2,$$所以$$k_{CD}=-\dfrac{1}{x_1+x_2},$$于是 $CD$ 的方程为$$y-\dfrac{y_1+y_2}{2}=-\dfrac{1}{x_1+x_2}\left(x-\dfrac{x_1+x_2}{2}\right).$$令 $x=0$,得点 $D$ 坐标为 $D\left(0,\dfrac{y_1+y_2}{2}+\dfrac12\right)=\left(0,\dfrac54\right)$,所以 $OD=\dfrac54$.
因为 $AB$ 过焦点 $F$,所以 $AB$ 的方程为$$y-\dfrac14=(x_1+x_2)\cdot x.$$将点 $C$ 坐标代入,得$$y_1+y_2=(x_1+x_2)^2+\dfrac12,$$所以$$k_{AB}=x_1+x_2=\pm1,$$故 $OD$ 与 $AB$ 相交成 $45^\circ$ 锐角.
因此四边形 $AOBD$ 的面积为$$S=\dfrac12\cdot AB\cdot OD\cdot\sin45^\circ=\dfrac{5\sqrt2}{8}.$$
由条件知,抛物线的焦点为 $F\left(0,\dfrac14\right)$,准线方程为 $y=-\dfrac14$.
根据抛物线定义得,$$AF=y_1+\dfrac14,BF=y_2+\dfrac14,$$所以$$2=AF+BF=y_1+y_2+\dfrac12,y_1+y_2=\dfrac32.$$$AB$ 的中点为 $C\left(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2}\right)$,又因为$$k_{AB}=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{x_2^2-x_1^2}{x_2-x_1}=x_1+x_2,$$所以$$k_{CD}=-\dfrac{1}{x_1+x_2},$$于是 $CD$ 的方程为$$y-\dfrac{y_1+y_2}{2}=-\dfrac{1}{x_1+x_2}\left(x-\dfrac{x_1+x_2}{2}\right).$$令 $x=0$,得点 $D$ 坐标为 $D\left(0,\dfrac{y_1+y_2}{2}+\dfrac12\right)=\left(0,\dfrac54\right)$,所以 $OD=\dfrac54$.
因为 $AB$ 过焦点 $F$,所以 $AB$ 的方程为$$y-\dfrac14=(x_1+x_2)\cdot x.$$将点 $C$ 坐标代入,得$$y_1+y_2=(x_1+x_2)^2+\dfrac12,$$所以$$k_{AB}=x_1+x_2=\pm1,$$故 $OD$ 与 $AB$ 相交成 $45^\circ$ 锐角.
因此四边形 $AOBD$ 的面积为$$S=\dfrac12\cdot AB\cdot OD\cdot\sin45^\circ=\dfrac{5\sqrt2}{8}.$$
答案
解析
备注