如图，锐角 $\triangle ABC$ 中，$T$ 是高线 $AD$ 上的任意一点，$BT$ 交 $AC$ 于 $E$，$CT$ 交 $AB$ 于 $F$，$EF$ 交 $AD$ 于 $G$，过点 $G$ 的一直线 $l$ 与 $AB,AC,BT,CT$ 相交，交点分别为 $M,N,P,Q$．证明：$\angle MDQ=\angle NDP$．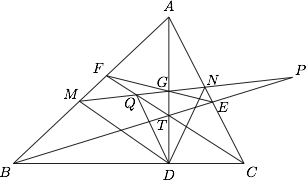
【难度】
【出处】
2012年全国高中数学联赛江西省预赛
【标注】
【答案】
略
【解析】
$CF$ 截 $\triangle ABE$，得$$\dfrac{AC}{CE}\cdot\dfrac{ET}{TB}\cdot\dfrac{BF}{FA}=1.$$又由 $BC$ 截 $\triangle ATE$，得$$\dfrac{AD}{DT}\cdot\dfrac{TB}{BE}\cdot\dfrac{EC}{CA}=1,$$即$$\dfrac{AD}{DT}=\dfrac{BE\cdot AC}{BT\cdot CE}.$$由 $EF$ 截 $\triangle ABT$，则有$$\dfrac{TG}{GA}\cdot\dfrac{AF}{FB}\cdot\dfrac{BE}{ET}=1,$$即$$\dfrac{TG}{GA}=\dfrac{BF\cdot ET}{AF\cdot BE},$$所以$$\dfrac{AD\cdot TG}{DT\cdot AG}=\dfrac{AC}{CE}\cdot\dfrac{ET}{TB}\cdot\dfrac{BF}{FA}=1,$$因此$$AD\cdot TG=AG\cdot TD.\qquad\cdots\cdots\text{ ① }$$由于$$\dfrac{GA}{GT}=\dfrac{S_{\triangle BGA}}{S_{\triangle BGT}},\dfrac{GP}{GM}=\dfrac{S_{\triangle BGP}}{S_{\triangle BGM}},\dfrac{BP}{BT}=\dfrac{S_{\triangle GBP}}{S_{\triangle GBT}},$$所以$$\dfrac{GA}{GT}\cdot\dfrac{GP}{GM}=\dfrac{AB}{BM}\cdot\dfrac{BP}{BT}.\qquad\cdots\cdots\text{ ② }$$根据 ① 有$$\dfrac{GA}{GT}=\dfrac{AD}{DT}.$$又过点 $M,P$ 分别作 $BC$ 的垂线，垂足分别为 $R,H$，如图
因为$$\dfrac{GP}{GM}=\dfrac{DH}{DR},\dfrac{AB}{BM}=\dfrac{AD}{MR},\dfrac{BP}{BT}=\dfrac{PH}{TD},$$所以 ② 化为 $\dfrac{PH}{MR}=\dfrac{DH}{DR}$，故$$\mathrm{Rt}\triangle MDR\backsim\triangle PDH,$$从而 $\angle MDR=\angle PDH$，即 $\angle TDM=\angle TDP$．
又据对称性，有$$\angle TDH=\angle TDQ,$$因此 $\angle MDQ=\angle NDP$．
因为$$\dfrac{GP}{GM}=\dfrac{DH}{DR},\dfrac{AB}{BM}=\dfrac{AD}{MR},\dfrac{BP}{BT}=\dfrac{PH}{TD},$$所以 ② 化为 $\dfrac{PH}{MR}=\dfrac{DH}{DR}$，故$$\mathrm{Rt}\triangle MDR\backsim\triangle PDH,$$从而 $\angle MDR=\angle PDH$，即 $\angle TDM=\angle TDP$．又据对称性，有$$\angle TDH=\angle TDQ,$$因此 $\angle MDQ=\angle NDP$．
答案
解析
备注
