已知抛物线 $C:y^2=2px$ 过点 $P(1,1)$,过点 $\left(0,\dfrac 12\right)$ 作直线 $l$ 与抛物线 $C$ 交于不同的两点 $M,N$.过点 $M$ 作 $x$ 轴的垂线分别与直线 $OP,ON$ 交于点 $A,B$,其中 $O$ 为原点.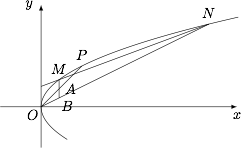

【难度】
【出处】
无
【标注】
-
求抛物线 $C$ 的方程,并求其焦点坐标和准线方程;标注答案焦点坐标为 $\left(\dfrac 14,0\right)$,准线方程为 $x=-\dfrac14$解析根据题意可得 $p=\dfrac 12$,于是抛物线 $C$ 的方程为 $y^2=x$,焦点坐标为 $\left(\dfrac 14,0\right)$,准线方程为 $x=-\dfrac14$.
-
求证:$A$ 为线段 $BM$ 的中点.标注答案略解析设 $M(m^2,m)$,$N(n^2,n)$,则\[\dfrac{m^2\cdot n-n^2\cdot m}{m^2-n^2}=\dfrac 12,\]即\[\dfrac 1m+\dfrac 1n=2.\]此时 $A\left(m^2,m^2\right)$,$B\left(m^2,\dfrac{m^2}{n}\right)$,因此 $A$ 为线段 $BM$ 的中点即\[m+\dfrac{m^2}{n}=2m^2,\]这显然成立,原命题得证.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2