在平面直角坐标系 $xOy$ 中，椭圆 $E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$（$a>b>0$）的离心率为 $\dfrac{\sqrt 2}2$，焦距为 $2$．
【难度】
【出处】
无
【标注】
-
求椭圆 $E$ 的方程；标注答案$\dfrac{x^2}2+y^2=1$解析略
-
如图，动直线 $l:y=k_1x-\dfrac{\sqrt 3}2$ 交椭圆 $E$ 于 $A,B$ 两点，$C$ 是椭圆 $E$ 上一点，直线 $OC$ 的斜率为 $k_2$，且 $k_1k_2=\dfrac{\sqrt 2}4$．$M$ 是线段 $OC$ 延长线上一点，且 $|MC|:|AB|=2:3$，圆 $M$ 的半径为 $|MC|$，$OS,OT$ 是圆 $M$ 的两条切线，切点分别为 $S,T$．求 $\angle SOT$ 的最大值，并求取得最大值时直线 $l$ 的斜率．
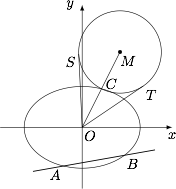标注答案$\angle SOT$ 的最大值为 $\dfrac{\pi}3$，此时直线 $l$ 的斜率为 $\pm \dfrac{\sqrt 2}2$解析设 $\angle SOM=\theta$，则 $\angle SOT=2\theta$，且\[\sin\theta=\dfrac{|MC|}{|OM|}=\dfrac{\dfrac 23|AB|}{|OC|+\dfrac 23|AB|}=\dfrac{2}{2+3\cdot \dfrac{|OC|}{|AB|}}.\]联立直线 $l$ 与椭圆 $E$ 的方程，可得\[\left(\dfrac 12+k_1^2\right)x^2-\sqrt 3k_1x-\dfrac 14=0,\]因此\[|AB|=\sqrt{1+k_1^2}\cdot \dfrac{\sqrt{4k_1^2+\dfrac 12}}{\dfrac 12+k_1^2}.\]联立直线 $y=k_2x$ 与椭圆 $E$ 的方程，可得\[\left(\dfrac 12+k_2^2\right)x^2=1,\]因此\[|OC|=\sqrt{1+k_2^2}\cdot \dfrac{1}{\sqrt{\dfrac 12+k_2^2}}=\dfrac{\sqrt{k_1^2+k_1^2k_2^2}}{\sqrt{\dfrac 12k_1^2+k_1^2k_2^2}}=\dfrac{\sqrt{k_1^2+\dfrac 18}}{\sqrt{\dfrac 12k_1^2+\dfrac 18}}.\]这样就有\[\begin{split}
\dfrac{|OC|}{|AB|}&=\dfrac{\sqrt{k_1^2+\dfrac 18}}{\sqrt{\dfrac 12k_1^2+\dfrac 18}}\cdot \dfrac{\dfrac 12+k_1^2}{\sqrt{1+k_1^2}\cdot \sqrt{4k_1^2+\dfrac 12}}\\
&=\dfrac{1}{\sqrt 2}\cdot \dfrac{k_1^2+\dfrac 12}{\sqrt{k_1^2+\dfrac 14}\cdot \sqrt{k_1^2+1}}\\
&=\dfrac{1}{\sqrt 2}\cdot \sqrt {1-\dfrac{1}{4k_1^2+\dfrac{1}{k_1^2}+5}}\\
&\geqslant \dfrac{1}{\sqrt 2}\cdot \sqrt{1-\dfrac{1}{2\sqrt{4k_1^2\cdot \dfrac{1}{k_1^2}}+5}}\\
&=\dfrac 23
,\end{split}\]等号当且仅当 $k_1^2=\dfrac 12$ 时取得．因此 $\sin\theta$ 的最大值为\[\dfrac{2}{2+3\cdot \dfrac 23}=\dfrac 12,\]继而 $\angle SOT$ 的最大值为 $\dfrac{\pi}3$，此时直线 $l$ 的斜率为 $\pm \dfrac{\sqrt 2}2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
