设椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$（$a>b>0$）的左焦点为 $F$，右顶点为 $A$，离心率为 $\dfrac 12$．已知 $A$ 是抛物线 $y^2=2px$（$p>0$）的焦点，$F$ 到抛物线的准线 $l$ 的距离为 $\dfrac 12$．
【难度】
【出处】
无
【标注】
-
求椭圆的方程和抛物线的方程；标注答案$x^2+\dfrac{4y^2}3=1$，$y^2=4x$解析根据题意，抛物线的准线 $l$ 过椭圆的左顶点，因此有\[\begin{cases}\dfrac ca=\dfrac 12,\\ a-c=\dfrac 12,\end{cases}\]其中 $c$ 为椭圆的半焦距．解方程，可得椭圆的方程为 $x^2+\dfrac{4y^2}3=1$，抛物线的方程为 $y^2=4x$．
-
设 $l$ 上两点 $P,Q$ 关于 $x$ 轴对称，直线 $AP$ 与椭圆相交于点 $B$（$B$ 异于点 $A$），直线 $BQ$ 与 $x$ 轴相交于点 $D$，若 $\triangle APD$ 的面积为 $\dfrac{\sqrt 6}2$，求直线 $AP$ 的方程．标注答案$y=-\dfrac{\sqrt 6}2x+\dfrac{\sqrt 6}2$ 或 $y=\dfrac{\sqrt 6}2x-\dfrac{\sqrt 6}2$解析如图．
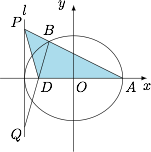考虑到图形的对称性，先计算 $B$ 点纵坐标为正实数的情形．设 $B\left(\cos\theta,\dfrac{\sqrt 3}2\sin \theta\right)$，$P(-1,m)$，则\[\dfrac{m-0}{-1-1}=\dfrac{\dfrac{\sqrt 3}2\sin\theta-0}{\cos\theta-1},\]解得\[m=\dfrac{\sqrt{3}\sin\theta}{1-\cos\theta}.\]于是 $Q\left(-1,\dfrac{\sqrt 3\sin\theta}{\cos\theta-1}\right)$，进而可得 $D$ 点的横坐标为\[\dfrac{\cos\theta\cdot \dfrac{\sqrt 3\sin\theta}{\cos\theta-1}-(-1)\cdot\dfrac{\sqrt 3}2\sin\theta}{\dfrac{\sqrt 3\sin\theta}{\cos\theta-1}-\dfrac{\sqrt 3}2\sin\theta}=\dfrac{3\cos\theta-1}{3-\cos\theta}.\]这样得到 $\triangle APD$ 的面积\[S=\dfrac 12\cdot \left(1-\dfrac{3\cos\theta-1}{3-\cos\theta}\right)\cdot \dfrac{\sqrt 3\sin\theta}{1-\cos\theta}=\dfrac{2\sqrt3\sin\theta}{3-\cos\theta}=\dfrac{\sqrt 6}2,\]解得 $\cos\theta=\dfrac 13$，$\sin\theta=\dfrac{2\sqrt 2}3$．进而可得直线 $AP$ 的方程为\[y=-\dfrac{\sqrt 6}2x+\dfrac{\sqrt 6}2.\]结合图形的对称性，可得直线 $AP$ 的方程为 $y=-\dfrac{\sqrt 6}2x+\dfrac{\sqrt 6}2$ 或 $y=\dfrac{\sqrt 6}2x-\dfrac{\sqrt 6}2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
