已知椭圆 $\dfrac {x^2}{a^2}+\dfrac {y^2}{b^2}=1(a>b>0)$ 的左焦点为 $F(-c,0)$，右顶点为 $A$，点 $E$ 的坐标为 $(0,c)$，$\triangle EFA$ 的面积为 $\dfrac {b^2}{2} $．
【难度】
【出处】
无
【标注】
-
求椭圆的离心率；标注答案$\dfrac 12$解析根据题意，有\[\dfrac 12\cdot (a+c)\cdot c=\dfrac 12b^2,\]从而 $a=2c$，离心率为 $\dfrac 12$．
-
设点 $Q$ 在线段 $AE$ 上，$|FQ|=\dfrac 32c$，延长线段 $FQ$ 与椭圆交于点 $P$，点 $M$，$N$ 在 $x$ 轴上，$PM \parallel QN$，且直线 $PM$ 与直线 $QN$ 间的距离为 $c$，四边形 $PQNM$ 的面积为 $3c$．
（i）求直线 $FP$ 的斜率；
（ii）求椭圆的方程．标注答案（i）$\dfrac{3}{4}$；（ii）$\dfrac{x^2}{16}+\dfrac{y^2}{12}=1$解析如图．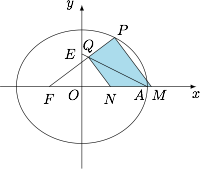
（i）根据题意，有 $A(2c,0)$，$E(0,c)$，$FQ=\dfrac 32c$，设 $\angle QFA=\theta$，则由 $E,Q,A$ 共线，可得\[\dfrac{\dfrac 32c\sin\theta}{\dfrac 32c\cos\theta-3c}=\dfrac{c}{-2c},\]解得 $\tan\theta=\dfrac 34$，直线 $FP$ 的斜率为 $\dfrac 34$．
（ii）由（i）可得 $Q\left(\dfrac 15c,\dfrac{9}{10}c\right)$．根据焦半径公式II，有\[PF=\dfrac{b^2}{a-c\cos\theta}=\dfrac{3c^2}{2c-\dfrac 45c}=\dfrac 52c,\]因此 $P\left(c,\dfrac 32c\right)$．注意到 $PQ=c$，于是 $PM,QN$ 均与 $PF$ 垂直，进而四边形 $PQNM$ 的面积\[\begin{split}S_{PQNM}&=S_{\triangle MPF}-S_{\triangle NQF}\\
&=\dfrac 12FP^2\tan\theta-\dfrac 12FQ^2\tan\theta\\
&=\dfrac 12\cdot \dfrac 34\cdot \left[\left(\dfrac 52c\right)^2-\left(\dfrac 32c\right)^2\right]\\
&=\dfrac {3c^2}2,\end{split}\]从而 $c=2$，椭圆的方程为 $\dfrac{x^2}{16}+\dfrac{y^2}{12}=1$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
