如图，在平面直角坐标系 $xOy$ 中，二次函数 $y=\dfrac{\sqrt 3}{2}x^2-\dfrac{\sqrt 3}{2}x-\sqrt 3$ 的图象与 $x$ 轴交于点 $A$ 和点 $C$（点 $A$ 在点 $C$ 的左侧），与 $y$ 轴交于点 $B$，点 $M\left(\dfrac 12,t\right)$ 为抛物线对称轴上的一个动点，连接 $MA,MB$，若 $\angle AMB$ 不小于 $60^\circ$，求 $t$ 的取值范围．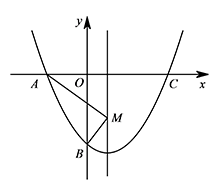
【难度】
【出处】
无
【标注】
【答案】
$t$ 的取值范围为 $\dfrac{-2\sqrt 3-\sqrt{39}}{6}\leqslant t \leqslant \dfrac{-2\sqrt 3+\sqrt {39}}{6}$
【解析】
因为 $y=\dfrac{\sqrt 3}2x^2-\dfrac{\sqrt 3}2x-\sqrt 3=\dfrac{\sqrt 3}2(x+1)(x-2)$，
所以点 $A,B$ 的坐标分别为 $(-1,0),(0,-\sqrt 3)$．
连接 $AB$，则 $\tan \angle ABO=\dfrac{AO}{BO}=\dfrac{\sqrt 3}3$，
所以 $\angle ABO=30^\circ$．
过 $AB$ 的中点 $D$ 作 $AB$ 的垂线，交 $y$ 轴与点 $P$．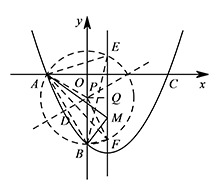
连接 $AP$，则 $AP=BP$ 且 $\angle APB=120^\circ$．
以点 $P$ 为圆心、$AP$ 长为半径作 $\odot P$，交抛物线对称轴于 $E,F$ 两点，连接 $AE,BE,AF,BF$，则 $\angle AEB=\angle AFB=\dfrac 12 \angle APB=60^\circ$．
所以当点 $M$ 在线段 $EF$ 上时，有 $\angle AMB\geqslant 60^\circ$．
过点 $P$ 作 $PQ\perp EF$ 于点 $Q$，则 $EQ=FQ=\dfrac 12 EF$，$PQ=\dfrac 12$．
连接 $PF$，则 $PF=PA=\dfrac{AO}{\frac {\sqrt 3}2}=\dfrac{2\sqrt 3}3$．
所以 $QF=\sqrt{PF^2-PQ^2}=\dfrac{\sqrt{39}}2$．
而 $OP=OB-PB=\dfrac{\sqrt 3}3$，所以点 $P$ 的坐标为 $\left(0,-\dfrac{\sqrt 3}3\right)$，
从而点 $Q$ 的坐标为 $\left(\dfrac 12,-\dfrac{\sqrt 3}3\right)$，
所以点 $E,F$ 的坐标分别为 $\left(\dfrac 12,\dfrac{-2\sqrt 3+\sqrt{39}}6\right),\left(\dfrac 12,\dfrac{-2\sqrt 3-\sqrt{39}}6\right)$．
综上可得，满足题意的 $t$ 的取值范围为 $\dfrac{-2\sqrt 3-\sqrt{39}}{6}\leqslant t \leqslant \dfrac{-2\sqrt 3+\sqrt {39}}{6}$．
所以点 $A,B$ 的坐标分别为 $(-1,0),(0,-\sqrt 3)$．
连接 $AB$，则 $\tan \angle ABO=\dfrac{AO}{BO}=\dfrac{\sqrt 3}3$，
所以 $\angle ABO=30^\circ$．
过 $AB$ 的中点 $D$ 作 $AB$ 的垂线，交 $y$ 轴与点 $P$．
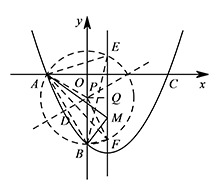连接 $AP$，则 $AP=BP$ 且 $\angle APB=120^\circ$．以点 $P$ 为圆心、$AP$ 长为半径作 $\odot P$，交抛物线对称轴于 $E,F$ 两点，连接 $AE,BE,AF,BF$，则 $\angle AEB=\angle AFB=\dfrac 12 \angle APB=60^\circ$．
所以当点 $M$ 在线段 $EF$ 上时，有 $\angle AMB\geqslant 60^\circ$．
过点 $P$ 作 $PQ\perp EF$ 于点 $Q$，则 $EQ=FQ=\dfrac 12 EF$，$PQ=\dfrac 12$．
连接 $PF$，则 $PF=PA=\dfrac{AO}{\frac {\sqrt 3}2}=\dfrac{2\sqrt 3}3$．
所以 $QF=\sqrt{PF^2-PQ^2}=\dfrac{\sqrt{39}}2$．
而 $OP=OB-PB=\dfrac{\sqrt 3}3$，所以点 $P$ 的坐标为 $\left(0,-\dfrac{\sqrt 3}3\right)$，
从而点 $Q$ 的坐标为 $\left(\dfrac 12,-\dfrac{\sqrt 3}3\right)$，
所以点 $E,F$ 的坐标分别为 $\left(\dfrac 12,\dfrac{-2\sqrt 3+\sqrt{39}}6\right),\left(\dfrac 12,\dfrac{-2\sqrt 3-\sqrt{39}}6\right)$．
综上可得，满足题意的 $t$ 的取值范围为 $\dfrac{-2\sqrt 3-\sqrt{39}}{6}\leqslant t \leqslant \dfrac{-2\sqrt 3+\sqrt {39}}{6}$．
答案
解析
备注
