查看数据源：59fad8786ee16400083d2859
在正四面体 $ABCD$ 中，点 $E$ 是 $BC$ 中点，$F$ 是 $AD$ 中点，$\overrightarrow{AF}$ 与 $\overrightarrow{CE}$ 所成角为 $\alpha$，则 $\cos \alpha=$  \((\qquad)\)
A: $\dfrac 12$
B: $-\dfrac 12$
C: $\dfrac 23$
D: $-\dfrac 23$
【难度】
【出处】
2010年第二十一届“希望杯”全国数学邀请赛高一（一试）
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何量
    >
    利用向量计算空间几何量
  • 知识点
    >
    立体几何
    >
    空间几何量
    >
    空间的角
    >
    异面直线所成的角
【答案】
D
【解析】
如图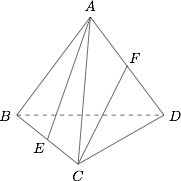．记 $\overrightarrow{AB}=\overrightarrow x$，$\overrightarrow{AC}=\overrightarrow y$，$\overrightarrow{AD}=\overrightarrow z$，则$$\overrightarrow{x}\cdot \overrightarrow y=\overrightarrow y\cdot \overrightarrow z=\overrightarrow z\cdot \overrightarrow x =2,\overrightarrow x^2+\overrightarrow y^2+\overrightarrow z^2=4.$$因为$$\overrightarrow{AE}=\dfrac{\overrightarrow x+\overrightarrow y}{2},\overrightarrow{CF}=\overrightarrow{AF}-\overrightarrow{AC}=\dfrac 12 \overrightarrow z-\overrightarrow y.$$所以\[\begin{split}\cos \alpha=\dfrac{\overrightarrow{AE}\cdot \overrightarrow{CF}}{\left|\overrightarrow{AE}\right|\left|\overrightarrow{CF}\right|}=-\dfrac{2}{3}.\end{split}\]
题目 答案 解析 备注
0.156508s