现有正方形 $ABCD$ 和一个以 $O$ 为直角顶点的三角板，移动三角板，使三角板两直角边所在直线分别与直线 $BC,CD$ 交于点 $M,N$．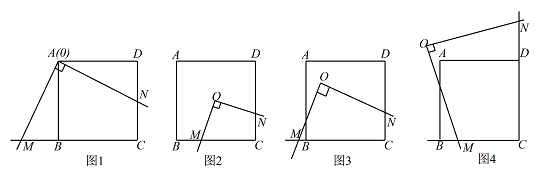
【难度】
【出处】
无
【标注】
-
如图1，若点 $O$ 与点 $A$ 重合，则 $OM$ 与 $ON$ 的数量关系是
-
如图2，若点 $O$ 在正方形的中心（即两对角线交点），则（$1$）中的结论是否仍然成立？请说明理由；标注答案$OM=ON$ 仍然成立解析如图2，过 $O$ 作 $OE\perp BC$ 于 $E$，$OF\perp CD$ 于 $F$．
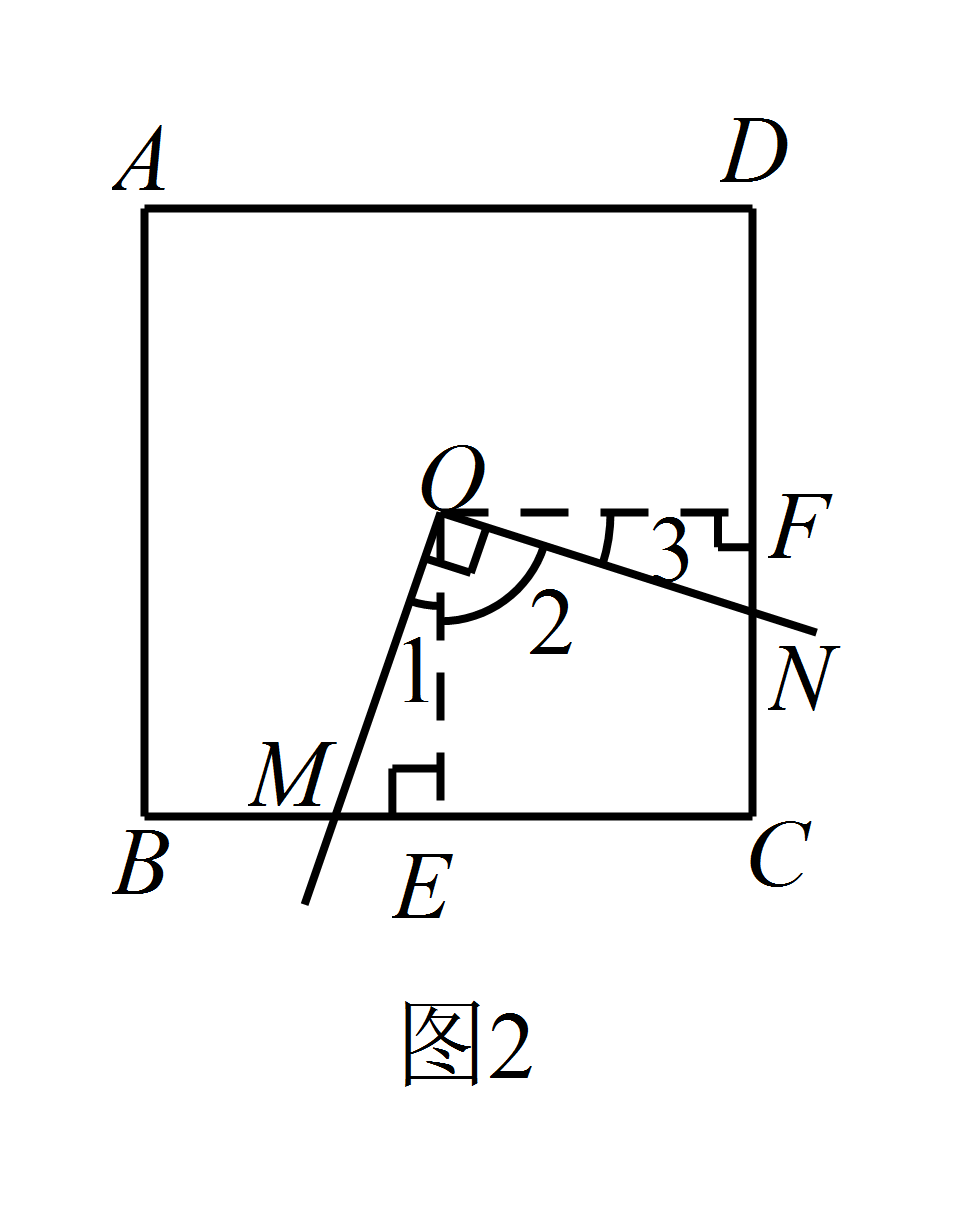所以 $\angle OEM=\angle OFN=90^{\circ}$．
因为 $O$ 是正方形 $ABCD$ 的中心，
所以 $OE=OF$．
因为 $\angle EOF=90^{\circ}$，
所以 $\angle 2+\angle 3=90^{\circ}$．
所以 $\angle 1+\angle 2=90^{\circ}$，
所以 $\angle 1=\angle 3$．
所以 $\triangle OEM\cong \triangle OFN$．
所以 $OM=ON$． -
如图3，若点 $O$ 在正方形的内部（含边界），当 $OM=ON$ 时，请探究点 $O$ 在移动过程中可形成什么图形？标注答案点 $O$ 在正方形内（含边界）移动所形成的图形是对角线 $AC$解析如图3，过 $O$ 作 $OE\perp BC$ 于 $E$，$OF\perp CD$ 于 $F$，
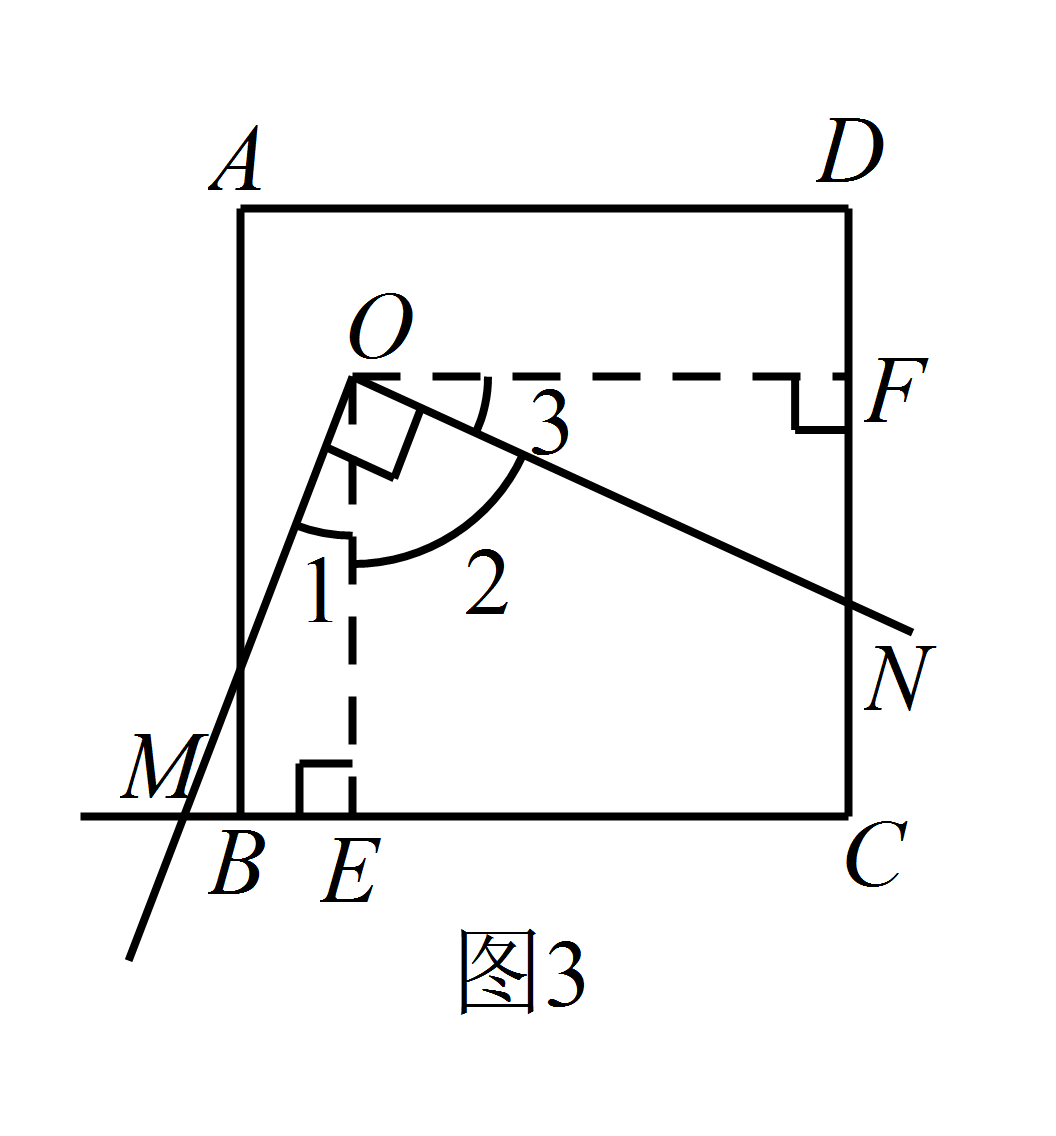所以 $\angle OEM=\angle OFN=90^{\circ}$．
因为 $\angle C=90^{\circ}$，
所以 $\angle 2+\angle 3=90^{\circ}$，
因为 $\angle 1+\angle 2=90^{\circ}$，
所以 $\angle 1=\angle 3$．
因为 $OM=ON$，
所以 $\triangle OEM\cong \triangle OFN$．
所以 $OE=OF$．
所以点 $O$ 在 $\angle BCD$ 的平分线上．
若点 $O$ 在 $\angle BCD$ 的平分线上，类似于（$2$）的证明可得 $OM=ON$．
所以点 $O$ 在正方形内（含边界）移动所形成的图形是对角线 $AC$． -
如图4，是点 $O$ 在正方形外部的一种情况．当 $OM=ON$ 时，请你就“点 $O$ 的位置在各种情况下（含外部）移动所形成的图形”提出一个正确的结论．（不必说理）标注答案所成图形为直线 $AC$解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
问题4
答案4
解析4
备注4
