如图，把 $\triangle EFP$ 放置在菱形 $ABCD$ 中，使得顶点 $E$，$F$，$P$ 分别在线段 $AB$，$AD$，$AC$ 上，已知 $EP=FP=6$，$EF=6\sqrt 3$，$\angle BAD=60^\circ$，且 $AB > 6\sqrt3$．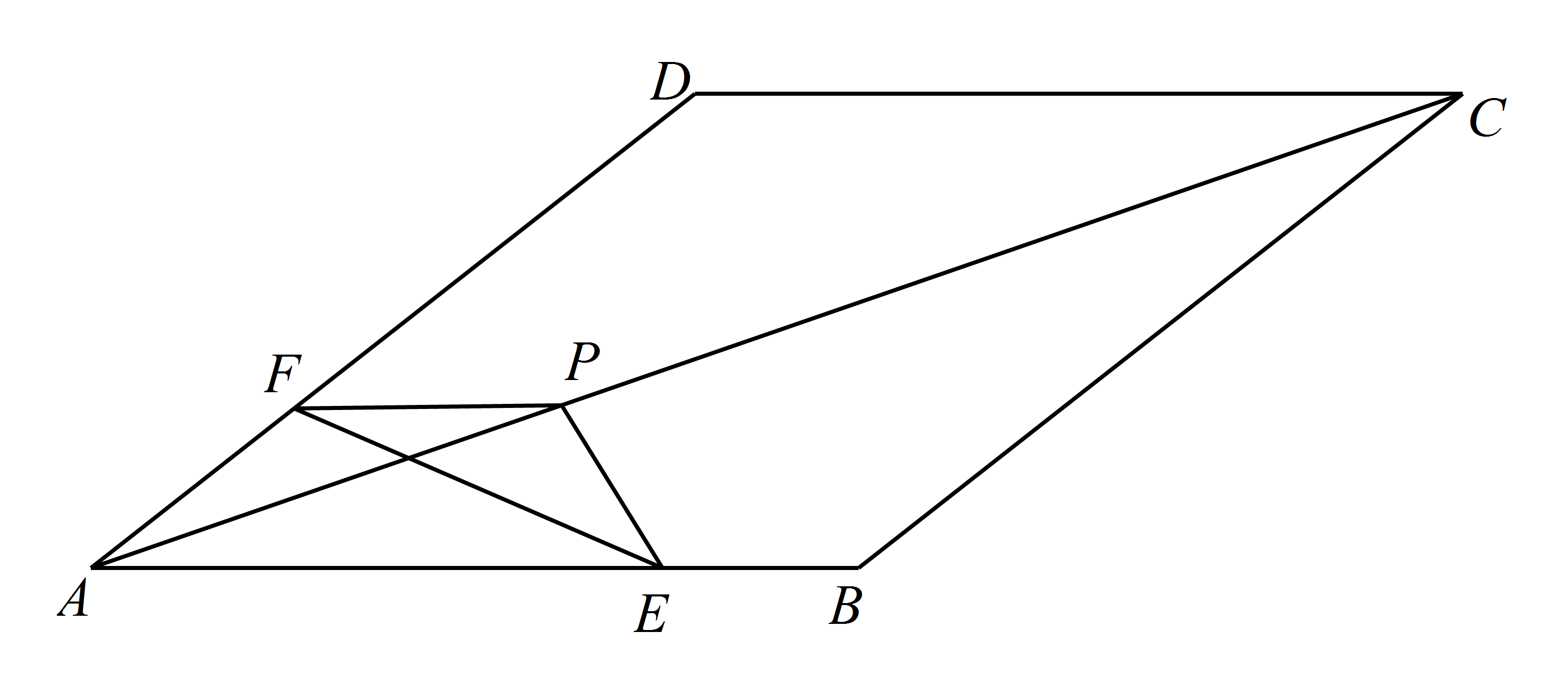
【难度】
【出处】
无
【标注】
-
$\angle EPF$ 的大小；标注答案$\angle EPF=120^\circ$解析如图，过点 $P$ 作 $PG \perp EF$ 于 $G$．
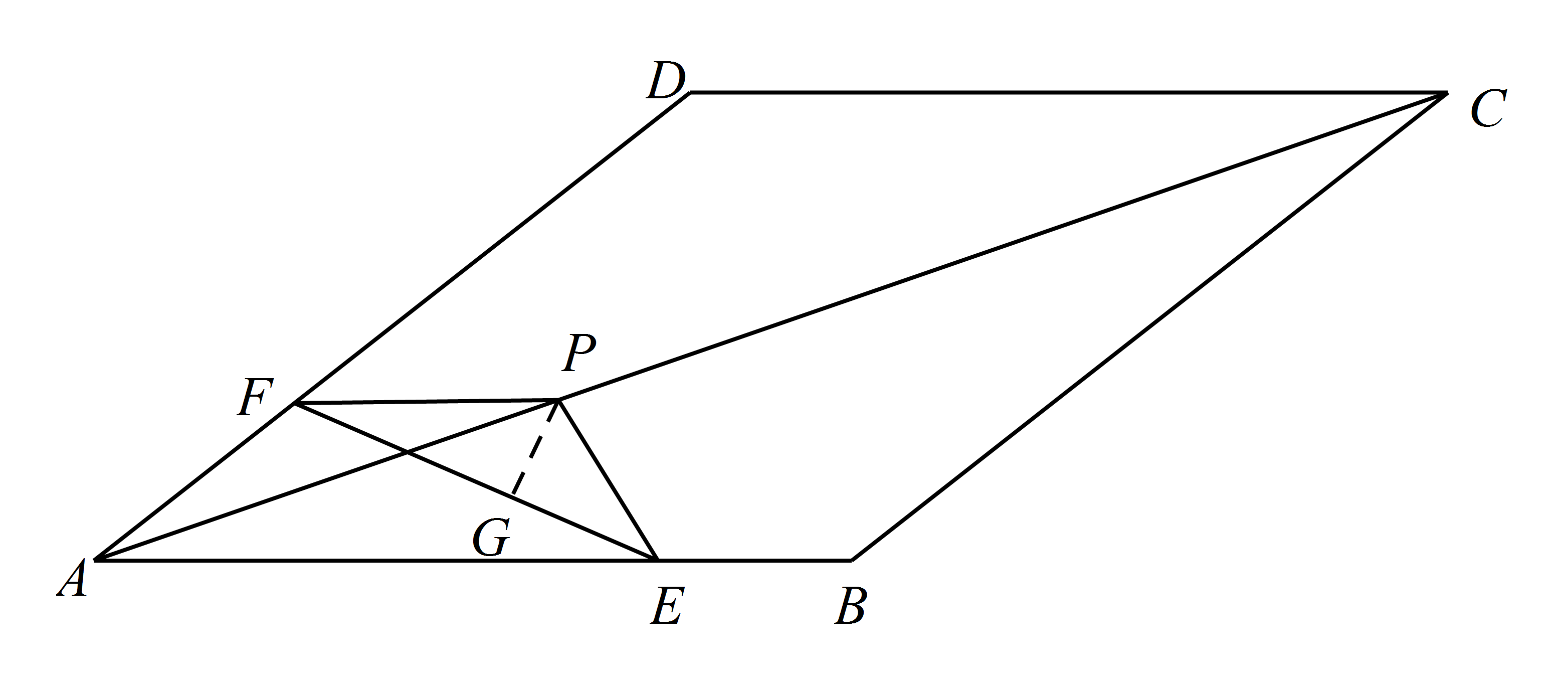因为 $PE=PF=6$，$EF=6\sqrt 3$，
所以 $FG=EG= 3\sqrt 3$，$\angle FPG=\angle EPG= \dfrac{\angle EPF}{2}$．
在 $\mathrm {Rt}\triangle FPG$ 中，$\sin \angle FPG = \dfrac{FG}{PF} = \dfrac{3\sqrt 3 }{6} = \dfrac{\sqrt 3 }{2}$．
所以 $\angle FPG=60^\circ$．
所以 $\angle EPF = 2\angle FPG = 120^\circ$． -
若 $AP=8$，求 $AE+AF$ 的值；标注答案$AE+AF=10\sqrt3$解析作 $PM\perp AB$ 于 $M$，$PN\perp AD$ 于 $N$．
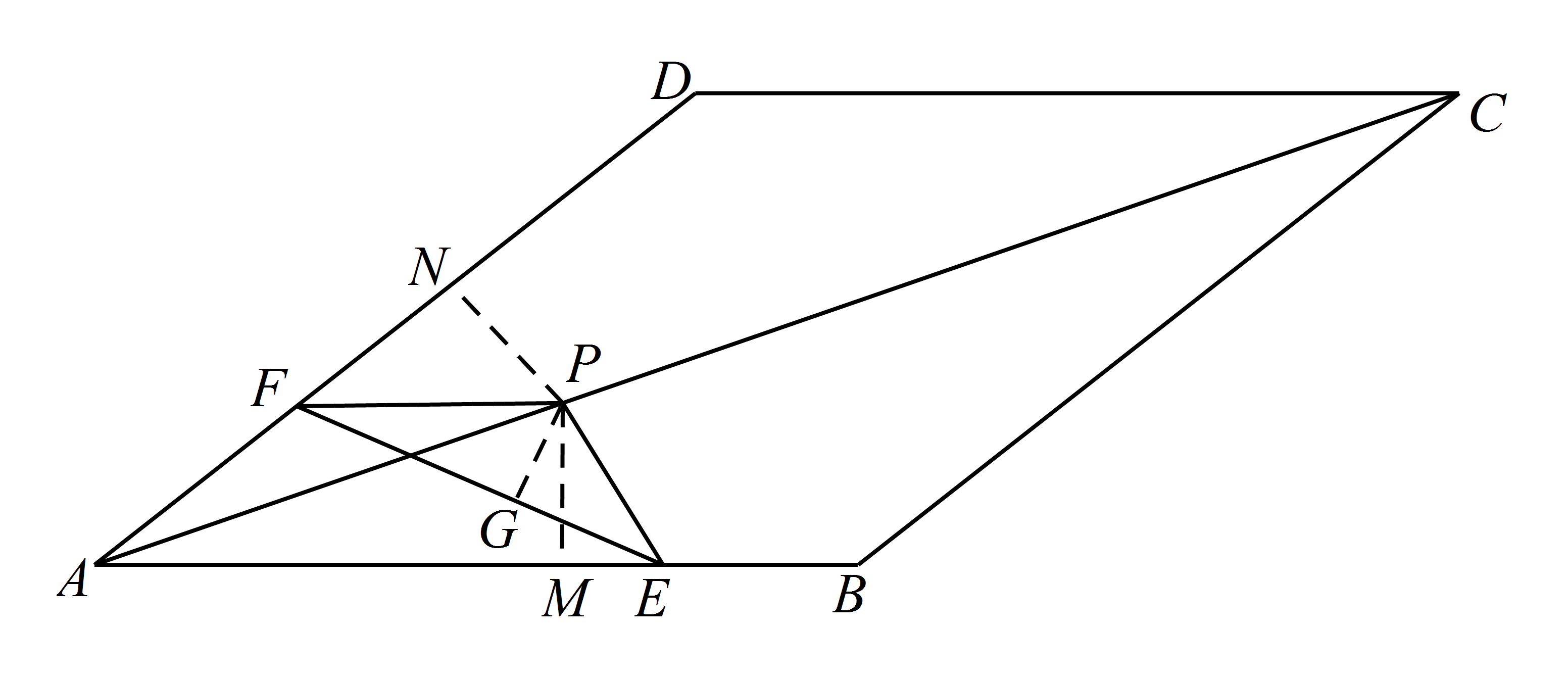因为 $AC$ 为菱形 $ABCD$ 的对角线，
所以 $\angle DAC=\angle BAC$，$PM=PN$．
所以 $AM=AN$．
在 $\mathrm {Rt}\triangle PME$ 和 $\mathrm {Rt}\triangle PNF$ 中，
$\begin{cases}PM=PN,\\PE=PF,\end{cases}$
所以 $\mathrm {Rt}\triangle PME\cong \mathrm {Rt}\triangle PNF$
所以 $NF= ME$．
又 $AP=10$，
所以 $AM = AN = AP\cdot\cos 30^{\circ}= 10 \times \dfrac{\sqrt 3 }{2}= 5\sqrt 3 $．
所以 $AE+AF=\left(AM+ME\right)+\left(AN-NF\right)=AM+AN= 10\sqrt3$． -
若 $\triangle EFP$ 的三个顶点 $E$，$F$，$P$ 分别在线段 $AB$，$AD$，$AC$ 上 运动，请直接写出 $AP$ 长的最大值和最小值．标注答案$AP$ 的最大值为 $12$，$AP$ 的最小值为 $6$解析① 当点 $F,A$ 重合时，点 $P$ 位于 $P_1$ 处，此时 $AP=AP_1=6$．
② 当 $EF\perp AC$ 时，点 $P$ 位于 $P_2$ 处，如图．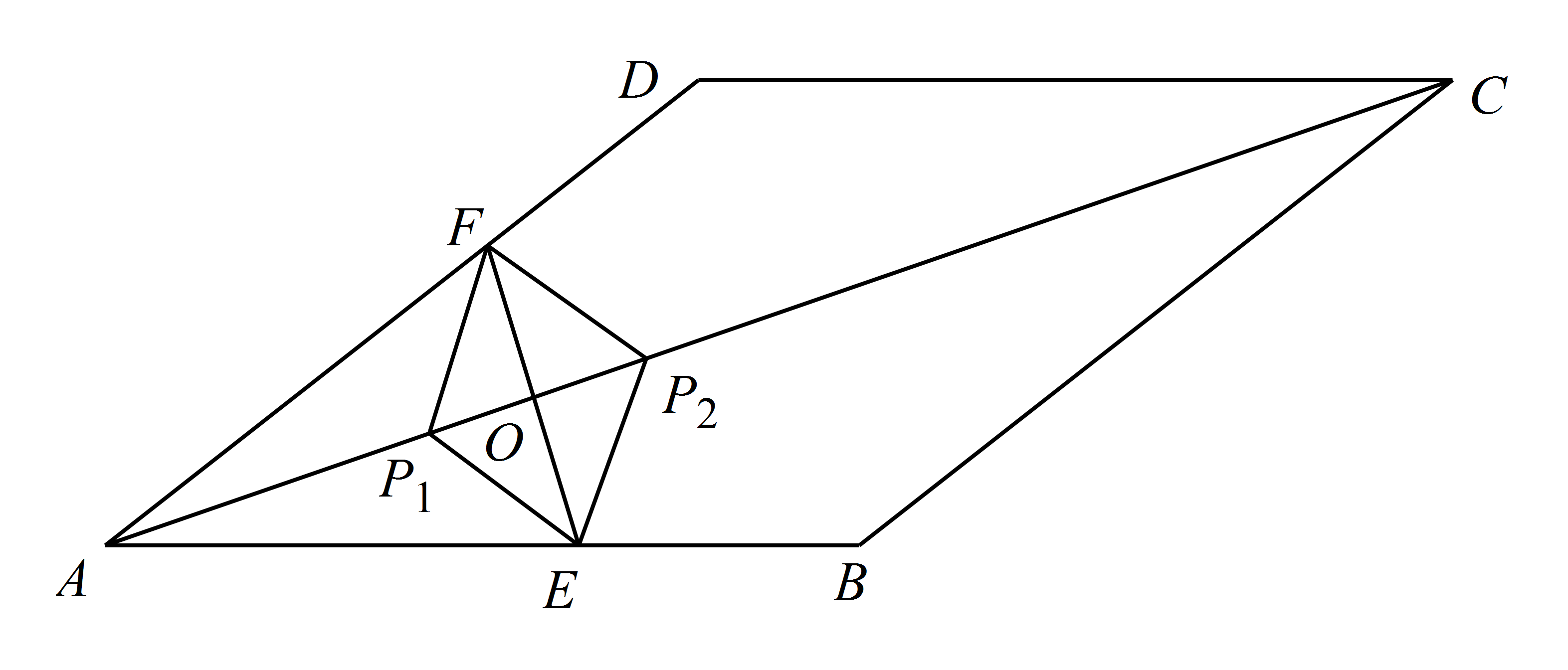
此时 $OF=3\sqrt{3}$．
所以 $AO=\sqrt{3}OF=9$，$ P_2O=\dfrac{\sqrt{3}}{3}OF=3$．
所以 $AP$ 的最大值为 $12$，$AP$ 的最小值为 $6$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
