如图，已知抛物线 $y=\dfrac 14x^2-\dfrac 14\left(b+1\right)x+\dfrac b4$（$b$ 是实数且 $b>2$）与 $x$ 轴的正半轴分别交于 $A,B$（点 $A$ 位于点 $B$ 的左侧），与 $y$ 轴的正半轴交于点 $C$．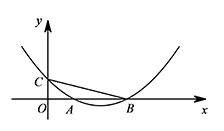
【难度】
【出处】
无
【标注】
-
求点 $B,C$ 的坐标（用 $b$ 表示）；标注答案点 $B$ 的坐标为 $\left(b,0\right)$，点 $C$ 的坐标为 $\left(0,\dfrac b4\right)$解析令 $y=0$，即 $\dfrac 14x^2-\dfrac 14\left(b+1\right)x+\dfrac b4=0$，
解得 $x=1$，$ x_2=b$．
因为 $b$ 是实数且 $b>2$，点 $A$ 位于点 $B$ 的左侧，
所以点 $B$ 的坐标为 $\left(b,0\right)$．
令 $x=0$，解得 $y=\dfrac b4$．
所以点 $C$ 的坐标为 $\left(0,\dfrac b4\right)$． -
第一象限内是否存在点 $Q$，使得 $\triangle QCO,\triangle QOA$ 和 $\triangle QAB$ 中的任意两个三角形均相似（全等可作相似的特殊情况）？如果存在，求出点 $Q$ 的坐标；如果不存在，请说明理由．标注答案存在，点 $Q\left(1,2+\sqrt 3\right)$ 或 $Q\left(1,4\right)$，使得 $\triangle QCO,\triangle QOA$ 和 $\triangle QAB$ 中的任意两个三角形均相似解析假设存在这样的点 $Q$，使得 $\triangle QCO,\triangle QOA$ 和 $\triangle QAB$ 中的任意三角形均相似．
因为 $\angle QAB=\angle AOQ+\angle AQO$，
所以 $\angle QAB>\angle AOQ$，$\angle QAB>\angle AQO$．
所以要使 $\triangle QOA$ 与 $\triangle QAB$ 相似，只能 $\angle QAO=\angle BAQ=90^\circ$，即 $QA\perp x$ 轴．
因为 $b>2$，
所以 $AB>OA$．
所以如图，只能 $\angle AOQ=\angle AQB$，此时 $\angle OQB=90^\circ$．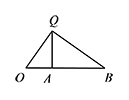
所以 $\triangle QOA\backsim \triangle BQA.$
所以只需讨论 $\triangle OQC$ 与 $\triangle QOA,\triangle BQA$ 相似的情况：
① 当 $\angle OCQ=90^\circ$ 时，$\triangle CQO\cong \triangle AOQ$，
所以 $AQ=CO=\dfrac b4$．
由 $QA^2=OA\cdot AB$ 得 $\left(\dfrac b4\right)^2=b-1$，
解得 $b=8\pm 4\sqrt 3$．
因为 $b>2$，
所以 $b=8+4\sqrt 3$．
所以点 $Q$ 的坐标是 $\left(1,2+\sqrt 3\right)$．
② 当 $\angle OQC=90^\circ$ 时，$\triangle OCQ\backsim \triangle QOA$，
所以 $\dfrac{OQ}{CO}=\dfrac{AQ}{QO}$，即 $OQ^2=OC\cdot AQ$．
又 $OQ^2=OA\cdot OB$，
所以 $OC\cdot AQ=OA\cdot OB$，即 $\dfrac b4\cdot AQ=1\cdot b$．
解得 $AQ=4$，
所以 $AB=16$，
此时 $b=17>2$ 符合条件．
所以点 $Q$ 的坐标是 $\left(1,4\right)$．
所以综上可知，存在点 $Q\left(1,2+\sqrt 3\right)$ 或 $Q\left(1,4\right)$，使得 $\triangle QCO,\triangle QOA$ 和 $\triangle QAB$ 中的任意两个三角形均相似．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
