在正方形 $ABCD$ 中，对角线 $AC$ 与 $BD$ 交于点 $O$；在 $\mathrm {Rt}\triangle PMN$ 中，$\angle MPN= 90^\circ$．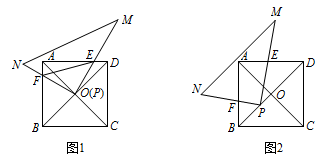
【难度】
【出处】
无
【标注】
-
如图 1，若 $\mathrm {Rt}\triangle PMN$ 的顶点 $P$ 与点 $O$ 重合，$PM,PN$ 分别交 $AD,AB$ 于点 $E,F$，请判断 $PE$ 与 $PF$ 的数量关系，并给出证明；标注答案$PE=PF$解析
解法一 $\because AC,BD$ 是正方形 $ABCD$ 的对角线，
$\therefore OA=OD$，$\angle FAO=\angle EDO=45^\circ$，$\angle AOD=90^\circ$，
$\therefore \angle DOE+\angle AOE=90^\circ$，
$\because \angle MPN=90^\circ$，
$\therefore \angle FOA+\angle AOE=90^\circ$，
$\therefore \angle FOA=\angle DOE$，
$\therefore \triangle FOA\cong \triangle EOD$，
$\therefore OE=OF$，即 $PE=PF$．解法二 如图，过点 $O$ 作 $AD,AB$ 的垂线，垂足分别为点 $G,H$．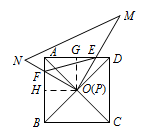
$\because$ 点 $O$ 为正方形 $ABCD$ 对角线的交点，
$\therefore OG=OH$，$\angle GOH=\angle EOF=90^\circ$，
$\therefore \angle EOG=\angle FOH$，
$\therefore \triangle EGO\cong \triangle FHO$，
$\therefore OE=OF$，即 $PE=PF$． -
如图2，若 $\mathrm {Rt}\triangle PMN$ 的顶点 $P$ 在线段 $OB$ 上移动（不与点 $O,B$ 重合），当 $BD=3BP$ 时，猜想此时 $PE$ 与 $PF$ 的数量关系，并给出证明；当 $BD=m\cdot BP$ 时，请直接写出 $PE$ 与 $PF$ 的数量关系．标注答案$PE=(m-1)\cdot PF$解析如图，过点 $P$ 作 $AD,AB$ 的垂线，垂足分别为点 $G,H$．
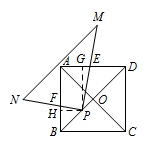则 $\angle GPH=\angle EPF=90^\circ$，
$\therefore \angle EPG=\angle FPH$，
$\therefore \triangle EGP \backsim \triangle FHP$，
$\therefore \dfrac{PE}{PF}=\dfrac{PG}{PH}$．
由 $BD=3BP$，可得 $PD=2PB$．
易证 $\triangle PHB\backsim \triangle PGD$，
$\therefore \dfrac{PE}{PF}=\dfrac{PG}{PH}=\dfrac{PD}{PB}=2$，
即 $PE=2PF$．
同理可得，当 $BD=m\cdot BP$ 时，有 $PE=(m-1)\cdot PF$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
