如图，等边 $\triangle ABC$ 中，点 $D$ 是 $BC$ 边的中点，点 $E,F$ 分别在边 $AB,AC$ 上，满足 $\angle EDF=120^\circ$．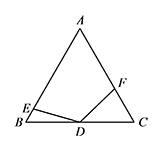
【难度】
【出处】
无
【标注】
-
证明：$DE=DF$；标注答案略解析如图，连接 $AD$，过点 $D$ 作 $AB,AC$ 的垂线，垂足分别为点 $G,H$．
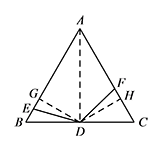由等腰三角形三线合一，可得到 $AD$ 平分 $\angle BAC$，
所以 $DG=DH$．
因为 $\angle EDF=120^\circ$，
所以 $\angle AED+\angle AFD=180^\circ$，
从而 $\angle AED=\angle CFD$，
所以 $\triangle DGE\cong \triangle DHF$，
所以 $DE=DF$． -
直接写出 $BE,CF,AB$ 之间的数量关系．标注答案$BE+CF=\dfrac 12 AB$解析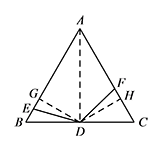由 $\triangle DGE\cong \triangle DHF$，可得 $EG=FH$．
易证 $\triangle DGB\cong \triangle DHC$，
所以 $BG=CH=\dfrac 12BD=\dfrac 14AB$．
所以 $BE+CF=2BG=\dfrac 12AB$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
