如图，在 $\triangle ABC$ 中，$\angle ACB=90^\circ$，以 $AB$ 为斜边作等腰直角 $\triangle ABD$，且点 $D$ 与点 $C$ 在直线 $AB$ 的两侧，连接 $CD$．
【难度】
【出处】
无
【标注】
-
若 $AC=1,BC=3$，求 $CD$ 的长；标注答案$CD=2\sqrt 2$解析
解法一 如图，延长 $CB$ 至点 $E$，使得 $BE=AC=1$，连接 $DE$．
由题意可得 $\angle ACB=\angle ADB=90^\circ$，
所以 $\angle DAC+\angle DBC=180^\circ$，
从而 $\angle DAC=\angle DBE$．
而 $DA=DB$，
所以 $\triangle DAC\cong \triangle DBE$，
所以 $CD=ED$，$\angle CDE=\angle ADB=90^\circ$，
所以 $CD=\dfrac{\sqrt 2}{2}CE=2\sqrt 2$．解法二 如图，过点 $D$ 作 $AC,BC$ 的垂线，垂足分别为点 $F,G$．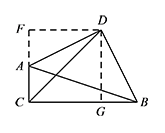
由题意可得 $\angle ACB=\angle ADB=90^\circ$，
所以 $\angle DAC+\angle DBC=180^\circ$，
从而 $\angle DAF=\angle DBG$．
而 $DA=DB$，
所以 $\triangle DFA\cong \triangle DGB$，
所以 $DF=DG$，$AF=BG$，
从而 $\angle DCH=\angle DCG=45^\circ$．
所以四边形 $CFDG$ 为正方形，$CG=CF=2$，
所以 $CD=2\sqrt 2$． -
用等式表示线段 $AC,BC,CD$ 之间的数量关系（直接写出即可）．标注答案$AC+BC=\sqrt 2CD$解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
