如图，在平面直角坐标系 $xOy$ 中，将抛物线 $y=x^2$ 的对称轴绕着点 $P\left(0,2\right)$ 顺时针旋转 $45^\circ $ 后与该抛物线交于 $A,B$ 两点，点 $Q$ 是该抛物线上的一点．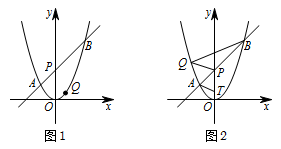
【难度】
【出处】
无
【标注】
-
如图1，若点 $Q$ 在直线 $AB$ 的下方，求点 $Q$ 到直线 $AB$ 的距离的最大值；标注答案点 $Q$ 到直线 $AB$ 距离的最大值为 $\dfrac{9\sqrt 2}{8}$解析如图，过点 $Q$ 作 $x$ 轴的垂线交 $AB$ 于点 $C$，再过点 $Q$ 作直线 $AB$ 的垂线，垂足为 $D$．
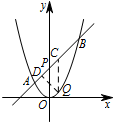由根据条件可得 $\angle APO=45^\circ$，
所以 $\angle DCQ=\angle APO=45^\circ$，
即 $\triangle QDC$ 为等腰直角三角形．
所以 $QD=\dfrac{\sqrt 2}{2}QC$，
故点 $QC$ 取最大值时，$QD$ 取最大值．
易得直线 $AP$ 的解析式为 $y=x+2$．
若设点 $Q\left(m,m^2\right)$，则点 $C\left(m,m+2\right)$，
所以 $QC=m+2-m^2=-\left(m-\dfrac 12\right)^2+\dfrac 94$，
所以 $QC$ 的最大值为 $\dfrac 94$，此时点 $Q\left(\dfrac 12,\dfrac 14\right)$．
所以 $QD$ 的最大值为 $\dfrac{9\sqrt 2}{8}$，
即点 $Q$ 到直线 $AB$ 距离的最大值为 $\dfrac{9\sqrt 2}{8}$． -
如图2，若点 $Q$ 在 $y$ 轴左侧，且点 $T\left(0,t\right)\left(t<2\right)$ 是直线 $PO$ 上一点，当以 $P,B,Q$ 为顶点的三角形与 $\triangle PAT$ 相似时，求所有满足条件的 $t$ 的值．标注答案$t$ 的值为 $t=1$ 或 $t=0$ 或 $t=1-\sqrt 3$ 或 $t=3-\sqrt 3$解析联立方程组 $\begin{cases}y=x^2,\\ y=x+2,\end{cases}$
解得 $\begin{cases}x_1=-1,\\y_1=1,\end{cases}\begin{cases}x_2=2,\\y_2=4.\end{cases}$
所以点 $A(-1,1)$，点 $B(2,4)$．
由 $\angle APT=45^\circ$，可得 $\triangle PBQ$ 中必有一个内角等于 $45^\circ$，由图知 $\angle BPQ=45^\circ$ 不合题意．
① 若 $\angle PBQ=45^\circ$，过点 $B$ 作 $x$ 轴的平行线，与抛物线和 $y$ 轴分别交于点 $Q_1,F$．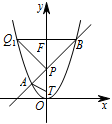
此时满足 $\angle PBQ_1=45^\circ$．
由抛物线的轴对称性，可得 $PB=PQ_1$，
所以 $\triangle BPQ_1$ 为等腰直角三角形，
则 $\triangle PAT$ 也为等腰直角三角形．
i）当 $\angle PTA$ 为直角时，得 $PT=AT=1$，此时 $t=1 $；
ii）当 $\angle PAT$ 为直角时，得 $PT=2$，此时 $t=0 $．
② 若 $\angle PQB=45^\circ$，① 中是情况之一，答案同上：
现以点 $F$ 为圆心，$FB$ 为半径作圆，则点 $P,B,Q_1$ 都在 $\odot F$ 上，设 $\odot F$ 与 $y$ 轴左侧的抛物线交于另一点 $Q_2$．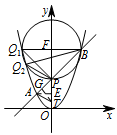
因为 $\angle PQ_2B$ 与 $ \angle PQ_1B $ 所对的弧相同，
所以 $\angle PQ_2B=\angle PQ_1B=45^\circ$，即这里的交点 $Q_2$ 也符合要求．
设点 $Q_2\left(n,n^2\right)\left(-2<n<0\right)$，
由 $FQ_2=2$，得 $n^2+\left(4-n^2\right)^2=2^2$，
整理得 $n^4-7n^2+12=0$，
解得 $n^2=3$ 或 $n^2=4$，
而 $-2<n<0$，故 $n=-\sqrt 3$，
即点 $Q_2\left(-\sqrt 3,3\right)$，
可证 $\triangle PFQ_2$ 为等边三角形，
所以 $\angle PBQ_2=\dfrac 12\angle PFQ_2=30^\circ$，
则在 $\triangle PQ_2B$ 中，$\angle PQ_2B=45^\circ$，$\angle PB Q_2=30^\circ$．
i）若 $\triangle Q_2PB\backsim\triangle PAT$，则过点 $A$ 作 $y$ 轴垂线，垂足为点 $E$．
则 $ET=\sqrt 3AE=\sqrt 3$，$OE=1$，
所以 $OT=\sqrt 3-1$，解得 $t=1-\sqrt 3$；
ii）若 $\triangle Q_2B P\backsim\triangle PAT$，则过点 $T$ 作直线 $AB$ 垂线，垂足为点 $G$．
设 $TG=a$，则 $PG=TG=a$，$AG=\sqrt 3TG=\sqrt 3a$，$AP=\sqrt 2$，
所以 $\sqrt 3a+a=\sqrt 2$，解得 $PT=\sqrt 2a=\sqrt 3-1$，
所以 $OT=OP-PT=3-\sqrt 3$，
即 $t=3-\sqrt 3$，
综上所述，所求 $t$ 的值为 $t=1$ 或 $t=0$ 或 $t=1-\sqrt 3$ 或 $t=3-\sqrt 3$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
