在 $\triangle ABC$ 中，$AB=AC$，点 $F$ 是 $BC$ 延长线上一点，以 $CF$ 为边，作菱形 $CDEF$，使菱形 $CDEF$ 与点 $A$ 在 $BC$ 的同侧，连接 $BE$，点 $G$ 是 $BE$ 的中点，连接 $AG,DG$．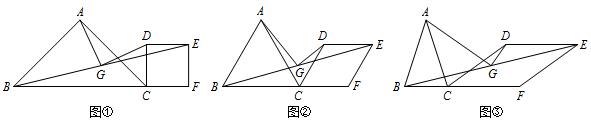
【难度】
【出处】
无
【标注】
-
如图1，当 $\angle BAC=\angle DCF=90^\circ$ 时，直接写出 $AG$ 与 $DG$ 的位置和数量关系；标注答案$AG\perp DG$，$AG=DG$解析延长 $DG$ 交 $BC$ 于点 $H$，连接 $AH,AD$．
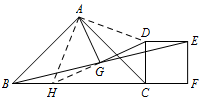易证 $\triangle BGH\cong\triangle EGD$，
所以 $HG=DG$，$BH=ED=CD$．
因为 $AB=AC$，$\angle BAC=\angle DCF=90^\circ$，
所以 $\angle ABH=\angle ACD=45^\circ$，
所以 $\triangle ABH\cong\triangle ACD$，
所以 $AH=AD$，$\angle BAH=\angle CAD$，
所以 $\angle HAD=\angle BAC=90^\circ$．
所以 $AG\perp DG$，$AG=DG$． -
如图2，当 $\angle BAC=\angle DCF=60^\circ$ 时，试探究 $AG$ 与 $DG$ 的位置和数量关系，并证明你的结论；标注答案$AG\perp DG$，$AG=\sqrt 3DG$（或 $DG=\dfrac{\sqrt 3}{3}AG$）解析延长 $DG$ 与 $BC$ 交于点 $H$，连接 $AH,AD$．
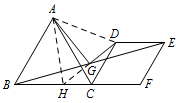易证 $\triangle BGH\cong \triangle EGD$，
所以 $HG=DG$，$BH=ED=CD$．
因为 $AB=AC$，$\angle BAC=\angle DCF=60^\circ$，
所以 $\angle ABH=\angle ACD=60^\circ$，
所以 $\triangle ABH\cong \triangle ACD$，
所以 $AH=AD$，$\angle BAH=\angle CAD$，
所以 $\angle HAD=\angle BAC=60^\circ$．
所以 $AG\perp HD$，$\angle HAG=\angle DAG=30^\circ$．
所以 $\dfrac{DG}{AG}=\tan \angle DAG=\tan 30^\circ=\dfrac{\sqrt 3}{3}$
所以 $AG=\sqrt 3DG$（或 $DG=\dfrac{\sqrt 3}{3}AG$）． -
当 $\angle BAC=\angle DCF=\alpha$ 时，直接写出 $AG$ 与 $DG$ 的数量关系．标注答案$DG=AG\tan \dfrac{\alpha}{2}$（或 $AG=DG\tan \left(90^\circ-\dfrac{\alpha}{2}\right)$）解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
