在 $\rm{Rt} \triangle ABC$ 中，$\angle ACB=90^\circ$，点 $D$ 与点 $B$ 在 $AC$ 同侧，$\angle DAC>\angle BAC$，且 $DA=DC$，过点 $B$ 作 $BE\parallel DA$ 交 $DC$ 于点 $E$，$M$ 为 $AB$ 的中点，连接 $MD,ME$．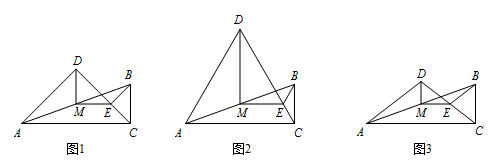
【难度】
【出处】
无
【标注】
-
如图1，当 $\angle ADC=90^\circ$ 时，线段 $MD$ 与 $ME$ 的数量关系是
-
如图3，当 $\angle ADC=\alpha$ 时，求 $\dfrac{ME}{MD}$ 的值．标注答案$\dfrac{ME}{MD}=\tan \dfrac{\alpha}{2}$解析延长 $EM$ 交 $DA$ 于点 $F$，
因为 $BE \parallel DA$，所以 $\angle FAM=\angle EBM$，
又因为 $AM=BM,\angle AMF=\angle BME$，
所以 $\triangle AMF\cong \triangle BME$，
所以 $AF=BE,MF=ME$，
延长 $BE$ 交 $AC$ 于点 $N$．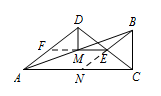
所以 $\angle BNC=\angle DAC$，
因为 $DA=DC$，所以 $\angle DCA=\angle DAC$，
所以 $\angle BNC=\angle DCA$，
因为 $\angle ACB=90^\circ$，所以 $\angle ECB=\angle EBC$，
所以 $CE=BE$，所以 $AF=CE$，
所以 $DF=DE$，所以 $DM\perp EF$，$DM$ 平分 $\angle ADC$，
因为 $\angle ADC=\alpha$，所以 $\angle MDE=\dfrac {\alpha}{2}$，
所以在 $\rm{Rt}\triangle MDE$ 中，$\dfrac{ME}{MD}=\tan \angle MDE=\tan \dfrac{\alpha}{2}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
