如图，四边形 $ABCD$ 的对角线 $AC,BD$ 相交于点 $O$，$OB=OD$，$OC=OA+AB$，$\angle ABD+\angle ADB=\angle ACB$，将 $\triangle ACD$ 沿 $CD$ 翻折，得到 $\triangle A'CD$，连接 $BA'$，与 $CD$ 相交于点 $P$，若 $CD=\dfrac{\sqrt 5+1}{2}$，求 $PC$ 的长．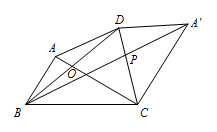
【难度】
【出处】
无
【标注】
【答案】
$PC=1$
【解析】
因为 $\angle ABD+\angle ADB=\angle ACB$，
所以 $\angle BAD+\angle ACB=180^\circ$，
作 $DE\parallel AB$ 交 $AC$ 于点 $E$．
所以 $\angle DEA=\angle BAE,\angle OBA=\angle ODE$，
又因为 $OB=OD$，
所以 $\triangle OAB\cong \triangle OED$，
所以 $AB=DE,OA=OE$，
所以设 $AB=DE=CE=x,OA=OE=y$，
因为 $\angle EDA+\angle DAB=180^\circ$，
所以 $\angle EDA=\angle ACB$，
因为 $\angle DEA=\angle EAB$，
所以 $\triangle EAD\backsim \triangle ABC$，
所以 $\dfrac{ED}{AC}=\dfrac{AE}{AB}=\dfrac{DA}{CB}=\dfrac mn$，
即 $\dfrac{x}{x+2y}=\dfrac{2y}{x}$，
所以 $4y^2+2xy-x^2=0$，即 $(\dfrac{2y}{x})^2+\dfrac{2y}{x}-1=0$，
所以 $\dfrac{2y}{x}=\dfrac{-1+\sqrt 5}{2}$，
所以 $\dfrac{AD}{BC}=\dfrac{-1+\sqrt 5}{2}$，
因为 $DE=CE,\angle DCA=\angle DCA'$，
所以 $DE\parallel CA'$，
因为 $AB\parallel DE$，
所以 $AB\parallel CA'$，
所以 $\angle ABC+\angle A'CB=180^\circ$，
所以 $A'D\parallel BC$，
所以 $\triangle PA'D\backsim \triangle PBC$，
所以 $\dfrac{PD}{PC}=\dfrac{A'D}{BC}$，
所以 $PC=1$．
所以 $\angle BAD+\angle ACB=180^\circ$，
作 $DE\parallel AB$ 交 $AC$ 于点 $E$．
所以 $\angle DEA=\angle BAE,\angle OBA=\angle ODE$，又因为 $OB=OD$，
所以 $\triangle OAB\cong \triangle OED$，
所以 $AB=DE,OA=OE$，
所以设 $AB=DE=CE=x,OA=OE=y$，
因为 $\angle EDA+\angle DAB=180^\circ$，
所以 $\angle EDA=\angle ACB$，
因为 $\angle DEA=\angle EAB$，
所以 $\triangle EAD\backsim \triangle ABC$，
所以 $\dfrac{ED}{AC}=\dfrac{AE}{AB}=\dfrac{DA}{CB}=\dfrac mn$，
即 $\dfrac{x}{x+2y}=\dfrac{2y}{x}$，
所以 $4y^2+2xy-x^2=0$，即 $(\dfrac{2y}{x})^2+\dfrac{2y}{x}-1=0$，
所以 $\dfrac{2y}{x}=\dfrac{-1+\sqrt 5}{2}$，
所以 $\dfrac{AD}{BC}=\dfrac{-1+\sqrt 5}{2}$，
因为 $DE=CE,\angle DCA=\angle DCA'$，
所以 $DE\parallel CA'$，
因为 $AB\parallel DE$，
所以 $AB\parallel CA'$，
所以 $\angle ABC+\angle A'CB=180^\circ$，
所以 $A'D\parallel BC$，
所以 $\triangle PA'D\backsim \triangle PBC$，
所以 $\dfrac{PD}{PC}=\dfrac{A'D}{BC}$，
所以 $PC=1$．
答案
解析
备注
