如图，在 $\triangle ABC$ 中，把 $AB$ 绕点 $A$ 顺时针旋转 $\alpha$ 得到 $AB'$，把 $AC$ 绕点 $A$ 逆时针旋转 $\beta$ 得到 $AC'$，连接 $B'C'$，$AD$ 是 $\triangle AB'C'$ 边 $B'C'$ 上的中线．当 $\alpha+\beta=180^\circ$ 时，猜想 $AD$ 与 $BC$ 的数量关系，并给予证明．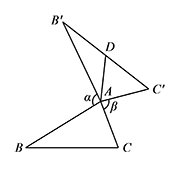
【难度】
【出处】
无
【标注】
【答案】
猜想 $BC=2AD$
【解析】
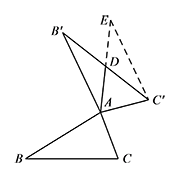易证 $\triangle ADB'\cong \triangle EDC'$，所以 $\angle E=\angle B'AE$，$C'E=AB'=AB$．
由 $\alpha+\beta=180^\circ$，可得 $\angle B'AC'+\angle BAC=180^\circ$．
又 $\angle E+\angle EAC'+\angle EC'A=180^\circ$，所以 $\angle EC'A=\angle BAC$．
而 $AC'=AC$，所以 $\triangle EC'A\cong \triangle BAC$，
从而 $BC=EA=2AD$．
显然 $\angle B'AF=\angle BAC$．而 $AB'=AB$，$AF=AC'=AC$，
所以 $\triangle ABC\cong \triangle AB'F$，
所以 $BC=B'F$．
因为 $DB'=DC'$，所以 $BC=B'F=2AD$．
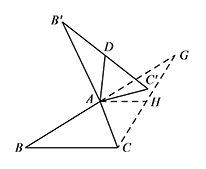显然 $\angle GAC=\angle B'AC'$．而 $AG=AB=AB'$，$AC=AC'$，
所以 $\triangle GAC\cong \triangle B'AC'$．
取 $CG$ 的中点，连接 $AH$，则 $AH=AD$．
所以 $BC=2AH=2AD$．
答案
解析
备注
