如图，$\triangle ABD$ 和 $\triangle ACE$ 都是直角三角形，其中 $\angle ABC=\angle ACE=90^\circ$，且点 $C$ 在 $AB$ 上，连接 $DE$，点 $M$ 为 $DE$ 的中点，连接 $BM,CM$，求证：$BM=CM$．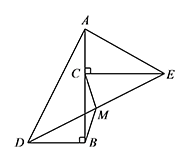
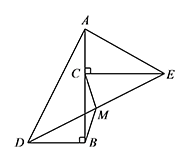
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
延长 $CM,DB$ 交于点 $F$，则 $\angle CBF=90^\circ$．
由题意可得 $CE\parallel DF$．
而点 $M$ 为 $DE$ 的中点，
所以 $\triangle CME\cong \triangle FMD$，
所以 $CM=FM$．
所以 $BM=\dfrac 12 CF=CM$．
由题意可得 $CE\parallel DF$．而点 $M$ 为 $DE$ 的中点，
所以 $\triangle CME\cong \triangle FMD$，
所以 $CM=FM$．
所以 $BM=\dfrac 12 CF=CM$．
答案
解析
备注
