如图，在 $\triangle ABC$ 中，$BC=22$，$BD\perp AC$ 于点 $D$，$CE\perp AB$ 于点 $E$，$F,G$ 分别是 $BC,DE$ 的中点，若 $ED=10$，求 $FG$ 的长．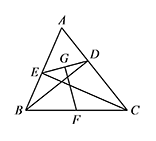
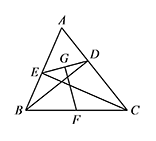
【难度】
【出处】
无
【标注】
【答案】
$FG=4\sqrt{6}$
【解析】
连接 $EF,DF$．
由题意可得 $EF,DF$ 分别为 $\mathrm{Rt}\triangle BEC,\mathrm{Rt}\triangle BDC$ 斜边的中线，
所以 $DF=EF=\dfrac 12BC=11$．
而点 $G$ 为 $DE$ 的中点，
所以 $DG=EG=5$，$FG\perp DE$．
所以在 $\mathrm{Rt}\triangle FGD$ 中，$FG=\sqrt{DF^2-DG^2}=4\sqrt{6}$．
由题意可得 $EF,DF$ 分别为 $\mathrm{Rt}\triangle BEC,\mathrm{Rt}\triangle BDC$ 斜边的中线，所以 $DF=EF=\dfrac 12BC=11$．
而点 $G$ 为 $DE$ 的中点，
所以 $DG=EG=5$，$FG\perp DE$．
所以在 $\mathrm{Rt}\triangle FGD$ 中，$FG=\sqrt{DF^2-DG^2}=4\sqrt{6}$．
答案
解析
备注
