如图，在四边形 $ABCD$ 中，点 $E,F$ 分别是 $AB,CD$ 的中点，过点 $E$ 作 $AB$ 的垂线，过点 $F$ 作 $CD$ 的垂线，两垂线交于点 $G$，连接 $AG,BG,CG,DG$，且 $\angle AGD=\angle BGC$．若 $AD,BC$ 所在的直线互相垂直，求 $\dfrac {AD}{EF}$．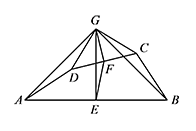
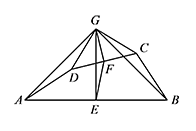
【难度】
【出处】
无
【标注】
【答案】
$\dfrac {AD}{EF}=\sqrt 2$
【解析】
由题意可得 $\triangle AGB$ 和 $\triangle DGC$ 为共顶点等顶角的两个等腰三角形，
所以 $\triangle AGD \cong \triangle BGC$，$\triangle AGD \sim \triangle EGF$．
解法一 连接 $CE$ 并延长至点 $H$，使得 $EH=EC$，连接 $AH$．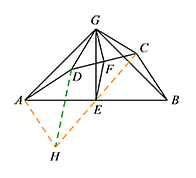
则 $AH \parallel BC,AH=BC$．
而 $AD=BC$，$AD\perp BC$，
所以 $AD=AH,AD\perp AH$．
连接 $DH$，则 $\triangle ADH$ 为等腰直角三角形．
又点 $E,F$ 为 $CH,CD$ 的中点，
所以 $\dfrac {AD}{EF}=\dfrac {AD}{\dfrac 12 DH}=\sqrt 2$．
解法二 如图，连接 $BD$ 并取中点 $H$，连接 $EH,FH$．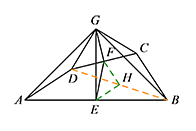
所以 $EH=\dfrac 12AD$ 且 $EH\parallel AD$，$FH=\dfrac 12BC$ 且 $FH\parallel BC$．
而 $AD=BC$，$AD\perp BC$．
所以 $\triangle EHF$ 为等腰直角三角形．
所以 $\dfrac {AD}{EF}=\dfrac {2EH}{EF}=\sqrt 2$．
所以 $\triangle AGD \cong \triangle BGC$，$\triangle AGD \sim \triangle EGF$．
则 $AH \parallel BC,AH=BC$．而 $AD=BC$，$AD\perp BC$，
所以 $AD=AH,AD\perp AH$．
连接 $DH$，则 $\triangle ADH$ 为等腰直角三角形．
又点 $E,F$ 为 $CH,CD$ 的中点，
所以 $\dfrac {AD}{EF}=\dfrac {AD}{\dfrac 12 DH}=\sqrt 2$．
所以 $EH=\dfrac 12AD$ 且 $EH\parallel AD$，$FH=\dfrac 12BC$ 且 $FH\parallel BC$．而 $AD=BC$，$AD\perp BC$．
所以 $\triangle EHF$ 为等腰直角三角形．
所以 $\dfrac {AD}{EF}=\dfrac {2EH}{EF}=\sqrt 2$．
答案
解析
备注
