如图，正方形 $ABCD$ 的边长为 $2$，$P$ 是射线 $CB$ 上一个动点，连接 $PA,PD$，点 $M,N$ 分别为 $BC,AP$ 的中点，连接 $MN$ 交 $PD$ 于点 $Q$，点 $P'$ 与点 $P$ 关于直线 $AB$ 对称，且点 $P'$ 在线段 $BC$ 上，连接 $AP'$，若点 $Q$ 恰好在直线 $AP'$ 上，求 $BP$ 的长．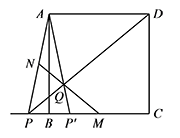
【难度】
【出处】
无
【标注】
【答案】
$BP=\sqrt 2-1$
【解析】
如图，延长 $MN,DA$ 交于点 $E$．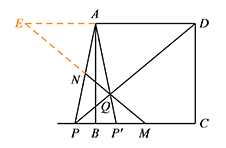
则 $\triangle AEN\cong \triangle PMN$，
所以 $AE=PM=BP+1$．
易证 $\triangle AQD\sim \triangle P'QP$，$\triangle EQD\sim \triangle MQP$，
所以 $\dfrac{PP'}{DA}=\dfrac {PQ}{DQ}=\dfrac{PM}{DE}$，
从而 $\dfrac {2BP}{2}=\dfrac{BP+1}{BP+3}$．
解得 $BP=\sqrt 2-1$．
则 $\triangle AEN\cong \triangle PMN$，所以 $AE=PM=BP+1$．
易证 $\triangle AQD\sim \triangle P'QP$，$\triangle EQD\sim \triangle MQP$，
所以 $\dfrac{PP'}{DA}=\dfrac {PQ}{DQ}=\dfrac{PM}{DE}$，
从而 $\dfrac {2BP}{2}=\dfrac{BP+1}{BP+3}$．
解得 $BP=\sqrt 2-1$．
答案
解析
备注
