我们把两条中线互相垂直的三角形称为“中垂三角形”．例如图 1，图 2，图 3 中，$AF$，$BE$ 是 $\triangle ABC$ 的中线，$AF\perp BE$，垂足为 $P$，像 $\triangle ABC$ 这样的三角形均为“中垂三角形”．设 $BC=a$，$AC=b$，$AB=c$．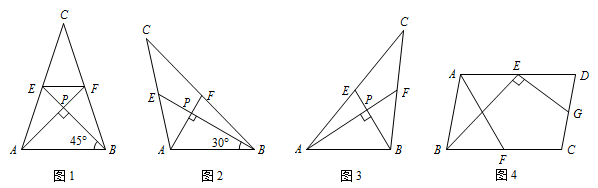
【难度】
【出处】
无
【标注】
-
特例探索：
（i）如图 1，当 $\angle ABE=45^\circ$，$c=2\sqrt 2$ 时，$a=$
（ii）如图 2，当 $\angle ABE=30^\circ$，$c=4$ 时，$a=$
（ii）$2\sqrt{13}$；$2\sqrt 7$解析略 -
归纳证明：请你观察第1问中的计算结果，猜想 $a^2,b^2,c^2$ 三者之间的关系，用等式表示出来，请利用图 3 证明你发现的关系式；标注答案猜想 $a^2,b^2,c^2$ 三者之间的关系是 $a^2+b^2=5c^2$解析如图，连接 $EF$，设 $AF$ 与 $BE$ 交于点 $P$．
因为 $AF,BE$ 是 $\triangle ABC$ 的中线，
所以 $EF$ 是 $\triangle ABC$ 的中位线．
所以 $EF\parallel AB$，且 $EF=\dfrac 12AB=\dfrac 12c$．
所以 $\dfrac{PE}{PB}=\dfrac{PF}{PA}=\dfrac 12$．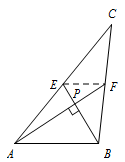
设 $PF=m$，$PE=n$，则 $AP=2m$，$PB=2n$，
在 $\mathrm {Rt}\triangle APB$ 中，$\left(2m\right)^2+\left(2n\right)^2=c^2; \quad \cdots \cdots ① $
在 $\mathrm {Rt}\triangle APE$ 中，$\left(2m\right)^2+n^2=\left(\dfrac b2\right)^2 ; \quad \cdots \cdots ② $
在 $\mathrm {Rt}\triangle BPF$ 中，$m^2+\left(2n\right)^2=\left(\dfrac a2\right)^2; \quad \cdots \cdots ③ $
由 ①，得 $m^2+n^2=\dfrac{c^2}{4}$．
由 ② $+$ ③，得 $5\left(m^2+n^2\right)=\dfrac{\left(a^2+b^2\right)}{4}$．
所以 $a^2+b^2=5c^2$． -
拓展应用：如图 4，在平行四边形 $ABCD$ 中，点 $E,F,G$ 分别是 $AD,BC,CD$ 的中点，$BE\perp EG$，$AD=2\sqrt 5$，$AB=3$．求 $AF$ 的长．标注答案$AF=4$解析
解法一 设 $AF,BE$ 交于点 $P$．如图，取 $AB$ 的中点 $H$，连接 $FH,AC$．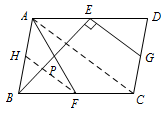
因为 $E,G$ 分别是 $AD,CD$ 的中点，$F$ 是 $BC$ 的中点，
所以 $EG\parallel AC\parallel FH$．
又 $ BE\perp EG$，
所以 $FH\perp BE$．
因为四边形 $ABCD$ 是平行四边形，
所以 $AD\parallel BC$，$AD=BC$．
所以 $AE=BF$，$AE\parallel BF$，
所以 $AP=FP$．
所以 $\triangle ABF$ 是“中垂三角形”．
所以 $AB^2+AF^2=5BF^2$，
即 $3^2+AF^2=5\left(\sqrt 5\right)^2$．
所以 $AF=4$．解法二 如图，连接 $AC,CE$，延长 $CE$ 交 $BA$ 的延长线于点 $H$．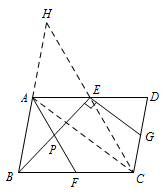
在 $\triangle ACD$ 中，
因为 $E,G$ 分别是 $AD,CD$ 的中点，
所以 $EG\parallel AC$．
因为 $BE\perp EG$，
所以 $AC\perp BE$．
因为平行四边形 $ABCD$，
所以 $AE\parallel BC$，$AD=BC$，$BC=2AE$．
所以 $\triangle HAE\backsim \triangle HBC$．
因为 $\dfrac{AE}{BC}=\dfrac{HA}{HB}=\dfrac{HE}{HC}=\dfrac 12$，
所以 $HA=AB$，$HE=EC$．
所以 $BE,CA$ 是 $\triangle HBC$ 的中线．
所以 $\triangle HBC$ 是中垂三角形．
所以 $HB^2+HC^2=5BC^2$．
因为 $AB=3$，$AE=\sqrt 5$，
所以 $HB=6$，$BC=2\sqrt 5$．
所以 $6^2+HC^2=5\times\left(2\sqrt 5\right)^2$，即 $HC=8$．
因为 $AF$ 是 $\triangle HBC$ 的中位线，
所以 $AF=\dfrac 12HC=4$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
