如图，在 $\triangle ABC$ 中，$\angle ACB=90^\circ$，$AC=BC=3$，$CE\perp AB$ 于点 $E$，点 $F$ 是 $CE$ 的中点，连接 $AF$ 并延长交 $BC$ 于点 $D$，$CG\perp AD$ 于点 $G$，连接 $EG$．
【难度】
【出处】
无
【标注】
-
求证：$BD=2DC$；标注答案略解析过点 $E$ 作 $EH\parallel AD$ 交 $BC$ 于点 $H$．
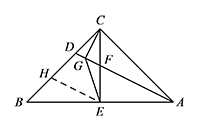由 $AC=BC$，$CE\perp AB$，可得 $AE=BE$，
所以 $\dfrac{BH}{DH}=\dfrac{BE}{AE}=1$，即 $BH=DH$．
而点 $F$ 是 $CE$ 的中点，
所以 $\dfrac{CD}{HD}=\dfrac{CF}{EF}=1$，即 $CD=HD$．
所以 $BD=2DC$． -
求 $EG$ 的长．标注答案$EG=\dfrac{3\sqrt 5}5$解析
解法一 因为 $CE\perp AB$，$CG\perp AD$，
所以 $\angle AEC=\angle AGC=90^\circ$，
从而 $A,E,G,C$ 四点共圆．
所以 $\angle AGE=\angle ACE=45^\circ=\angle B$，
所以 $\triangle AEG\backsim \triangle ADB$，
故有 $\dfrac{AE}{AD}=\dfrac{EG}{DB}$．
显然 $BD=\dfrac 23 BC=2$，$CD=\dfrac 13 BC=1$，
所以 $AD=\sqrt{DC^2+AC^2}=\sqrt{10}$．
而 $AE=\dfrac 12AB=\dfrac {\sqrt 2}2AC=\dfrac{3\sqrt 2}2$，
所以 $EG=\dfrac{AE}{AD}\cdot DB=\dfrac{\dfrac{3\sqrt 2}2}{\sqrt{10}}\times 2=\dfrac{3\sqrt 5}5$．解法二 延长 $CG$ 交 $EH$ 于点 $I$．
显然 $CI\perp EH$，$CG=IG$．
因为 $AC=3$，$CD=1$，$AD=\sqrt{10}$，
可得 $CG=\dfrac{AC\cdot DC}{AD}=\dfrac{3\sqrt{10}}{10}$．
同“解法一”可得 $A,E,G,C$ 四点共圆，
所以 $\angle EGI=\angle EAC=45^\circ$，
从而 $EG=\sqrt 2 IG=\dfrac{3\sqrt 5}5$．解法三 过点 $E$ 作 $JE\perp GE$ 交 $AD$ 于点 $J$．
由 $A,E,G,C$ 四点共圆，可得 $\angle EGA=45^\circ$．，
所以 $EG=EJ$，
从而 $\triangle EGC\cong \triangle EJA$，
所以 $AJ=CG=\dfrac{3\sqrt{10}}{10}$．
而 $\angle DCG=\angle DAC$，所以 $DG=\dfrac 13 CG=\dfrac{\sqrt{10}}{10}$，
故而 $GJ=AD-AJ-DG=\dfrac{3\sqrt{10}}{5}$，
所以 $EG=\dfrac{\sqrt 2}2GJ=\dfrac{3\sqrt 5}5$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
