在平行四边形 $ABCD$ 中，点 $B$ 关于 $AD$ 的对称点为 $B'$，连接 $AB',CB'$，$CB'$ 交 $AD$ 于 $F$ 点．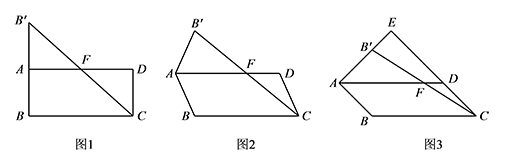
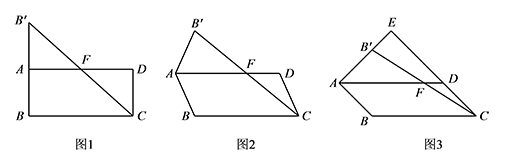
【难度】
【出处】
无
【标注】
-
如图1，$\angle ABC=90^\circ$，求证：$F$ 为 $CB'$ 的中点；标注答案略解析由四边形 $ABCD$ 为平行四边形，$\angle ABC=90^\circ$，
可得四边形 $ABCD$ 为矩形．
因为点 $B,B'$ 关于 $AD$ 对称，
所以 $\angle B'AD=\angle BAD=90^\circ$，$AB'=AB$．
而 $AD\parallel BC$，
所以 $\dfrac{FB'}{FC}=\dfrac{AB'}{AB}=1$，
即点 $F$ 为 $CB'$ 的中点． -
如图2，在点 $B$ 绕点 $A$ 旋转的过程中，求证：点 $F$ 始终为 $CB'$ 的中点．标注答案略解析
解法一 过点 $B'$ 作 $B'G\parallel CD$ 交 $AD$ 于点 $G$．
因为点 $B,B'$ 关于 $AD$ 对称，
所以 $\angle B'AD=\angle BAD$，$AB'=AB$．
因为 $AB\parallel CD$，$B'G\parallel CD$，
所以 $AB\parallel B'G$，
从而 $\angle B'GA=\angle BAD=\angle B'AG$，
所以 $B'G=B'A=BA=CD$，
所以 $\triangle B'GF\cong \triangle CDF$，
从而 $B'F=CF$，即点 $F$ 为 $B'C$ 的中点．解法二 连接 $BB'$ 交 $AD$ 于点 $H$．
因为点 $B,B'$ 关于 $AD$ 对称，
所以 $AD$ 垂直平分 $BB'$，
所以 $B'H=HB$．
因为 $AD\parallel BC$，
所以 $\dfrac{B'F}{FC}=\dfrac{B'H}{HB}=1$，
即点 $F$ 为 $CB'$ 的中点．解法三 连接 $BB',BF$．
因为点 $B,B'$ 关于 $AD$ 对称，
所以 $AD$ 垂直平分 $BB'$，
从而 $AD\perp BB'$，$FB=FB'$．
所以 $BB'\perp BC$，$\angle FBB'=\angle FB'B$．
所以 $\angle BB'F+\angle FCB=\angle B'BF+\angle FBC=90^\circ$，
所以 $\angle FBC=\angle FCB$，
从而 $FC=FB=FB'$，
即点 $F$ 为 $CB'$ 的中点． -
如图3，当 $\angle ABC=135^\circ$ 时，$AB',CD$ 的延长线相交于点 $E$，求 $\dfrac{CE}{AF}$ 的值．标注答案$\dfrac{CE}{AF}=\sqrt 2$解析因为四边形 $ABCD$ 为平行四边形，$\angle ABC=135^\circ$，
所以 $\angle BAD=\angle ADE=45^\circ$．
因为点 $B,B'$ 关于 $AD$ 对称，
所以 $\angle B'AD=\angle BAD=45^\circ$，
所以 $AB\perp AE$，$CE\perp AE$，
所以 $AE=DE$．
如图，过点 $F$ 作 $FG\parallel CE$．
易证 $AG=FG$，$FG\perp AG$，
所以 $AF=\sqrt 2 FG$．
由第2问可得，点 $F$ 为 $B'C$ 的中点，
所以 $CE=2FG$，
从而 $\dfrac{CE}{AF}=\dfrac{2FG}{\sqrt 2FG}=\sqrt 2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
