在 $\mathrm {Rt}\triangle ACB$ 和 $\mathrm {Rt}\triangle AEF$ 中，$\angle ACB=\angle AEF=90^\circ$，若 $P$ 是 $BF$ 的中点，连接 $PC,PE$．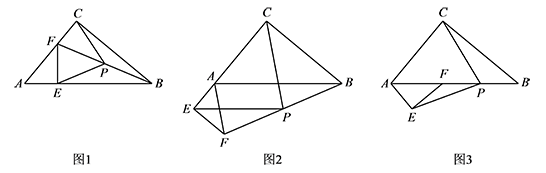
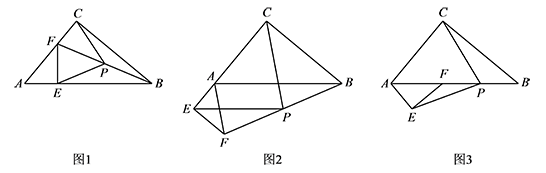
【难度】
【出处】
无
【标注】
-
如图1，若点 $E,F$ 分别落在边 $AB,AC$ 上，请直接写出此时线段 $PC$ 与 $PE$ 的数量关系；标注答案易得 $PC=PE=\dfrac 12 BF$，即 $PC$ 与 $PE$ 相等解析略
-
如图2，把图1中的 $\triangle AEF$ 绕着点 $A$ 顺时针旋转，当点 $E$ 落在边 $CA$ 的延长线上时，上述结论是否成立？若成立，请给予证明；若不成立，请说明理由；标注答案结论成立解析如图，延长 $CP$ 交 $EF$ 的延长线于点 $D$，则 $BC\parallel FD$．
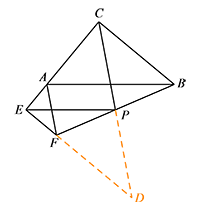易证 $\triangle BPC\cong \triangle FPD$，
所以 $PC=PD$．
而 $\angle CED=90^\circ$，
所以 $PE=\dfrac 12 CD=PC$． -
如图3，若点 $F$ 落在边 $AB$ 上，则上述结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由．标注答案结论仍然成立解析如图，过点 $F$ 作 $FD\parallel BC$，交 $CP$ 延长线于点 $D$，连接 $FD$．
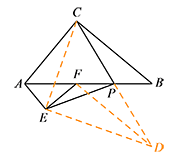易得 $PD=PC$，$FD=BC$．
所以 $\dfrac{AE}{AC}=\dfrac{EF}{CB}=\dfrac{FE}{FD}$．
而 $\angle AFE=\angle PBC=\angle PFD$，
所以 $\angle EAC=180^\circ-2\angle AFE=\angle EFD$．
连接 $CE,ED$．则 $\triangle EAC\sim\triangle EFD$，
所以 $\angle AEC=\angle FED$，$\angle CED=\angle AEF=90^\circ$．
所以 $PE=\dfrac 12 CD=PC$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
