已知 $\triangle ABC$ 和 $\triangle ADE$ 是等腰直角三角形，$\angle ACB=\angle ADE=90^\circ$，点 $F$ 为 $BE$ 中点，连接 $DF,CF$．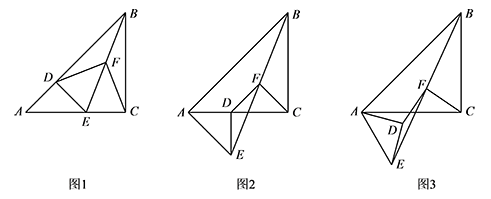
【难度】
【出处】
无
【标注】
-
如图1，当点 $D$ 在 $AB$ 上，点 $E$ 在 $AC$ 上，请直接写出此时线段 $DF,CF$ 的数量关系和位置关系（不用证明）；标注答案$DF=CF$，$DF\perp CF$解析因为 $\angle BDE=\angle BCE=90^\circ$，
所以 $DF=\dfrac 12 BE=CF$．
从而 $\angle DFE=2\angle DBE$，$\angle CFE=2\angle CBE$，
所以 $\angle DFC=2\angle DBC=90^\circ$，
即 $DF\perp CF$． -
如图2，在第1问的条件下将 $\triangle ADE$ 绕点 $A$ 顺时针旋转 $45^\circ$ 时，请你判断此时第1问中的结论是否仍然成立，并证明你的判断；标注答案第1问中的结论仍然成立解析如图，此时点 $D$ 落在 $AC$ 上，延长 $DF$ 交 $BC$ 于点 $G$．
易证 $DE\parallel BC$．
而点 $F$ 为 $BE$ 中点，
可得 $\triangle DEF\cong \triangle GBF$．
所以 $DA=DE=GB$，$DF=GF$．
而 $CA=CB$，
可得 $CD=CG$，即 $\triangle DCG$ 为等腰直角三角形，
所以 $DF=CF$，$DF\perp CF$． -
如图3，在第1问的条件下将 $\triangle ADE$ 绕点 $A$ 顺时针旋转 $\alpha$ 时，请你判断此时第1问中的结论是否仍然成立，并证明你的判断．标注答案第1问中的结论仍然成立解析延长 $CF$ 至 $G$，令 $FG=CF$，连接 $DG,EG,CD$．
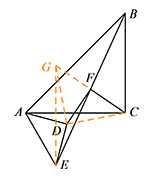易证 $\triangle EFG\cong\triangle BFC$，
所以 $BC=EG$，$BC\parallel EG$．
可得 $GE\perp AC$，
所以 $\angle DAC=\angle DEG$．
证得 $\triangle ADC\cong\triangle EDG$，
所以 $DG=DC$，$\angle EDG=\angle ADC$．
从而 $\angle GDC=\angle ADE=90^\circ$，即 $\triangle GCD$ 为等腰直角三角形，
所以 $DF=CF$，$DF\perp CF$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
