已知直线 $m\parallel n$，点 $C$ 是直线 $m$ 上一点，点 $D$ 是直线 $n$ 上一点，$CD$ 与直线 $m,n$ 不垂直，点 $P$ 为线段 $CD$ 的中点．
【难度】
【出处】
无
【标注】
-
如图1，直线 $l\perp m,l\perp n $，垂足分别为 $A,B$，连接 $PA,PB$，试判断线段 $PA$ 与 $PB$ 的数量关系并证明；标注答案$PA=PB$解析如图，延长 $AP$ 交直线 $n$ 于点 $E$．
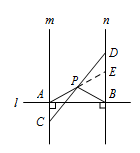因为 $m\parallel n$，
所以 $\dfrac{AP}{EP}=\dfrac{CP}{DP}$．
而 $CP=DP$，
所以 $AP=EP$．
因为 $n\perp l$，
所以在 $\mathrm{Rt}\triangle ABE$ 中，$BP=\dfrac 12 AE=AP$． -
在图1的情况下，把直线 $l$ 绕点 $A$ 旋转，使得 $\angle APB=90^\circ$（如图 2所示），若两平行线 $m,n$ 之间的距离为 $2k$．求证：$PA\cdot PB=k\cdot AB$．标注答案略解析如图，延长 $AP$ 交直线 $n$ 于点 $E$．
同第1问可证 $PA=PE$．
而 $PB\perp PA$，
所以 $AB=EB$．
过点 $A$ 作 $AF\perp n$ 于点 $F$，则 $AF=2k$．
因为 $S_{\triangle ABE}=\dfrac 12PB\cdot AE=\dfrac 12AF\cdot EB$，
即 $PB\cdot AE=AF\cdot EB$，
所以 $PB\cdot 2PA=2k\cdot AB$，
所以 $PA\cdot PB=k\cdot AB$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
