在锐角 $\triangle ABC$ 中，$AB=AC$，$AD$ 为 $BC$ 边上的高，$E$ 为 $AC$ 中点，若 $M$ 为线段 $BD$ 上的动点（点 $M$ 与点 $D$ 不重合），过点 $C$ 作 $CN\perp AM$ 于 $N$ 点，射线 $EN,AB$ 相交于 $P$ 点，证明 $\angle APE=2\angle MAD$．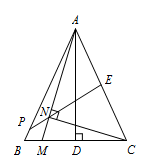
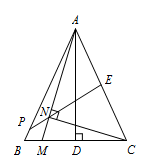
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
连接 $DE$．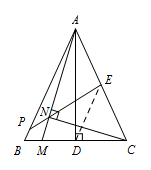
因为 $AB=AC$，$AD$ 为 $BC$ 边上的高，
所以 $D$ 为 $BC$ 中点，
因为 $E$ 为 $AC$ 中点，
所以 $ED\parallel AB$，
所以 $\angle DEP=\angle APE$，
因为 $\angle ADC=90^\circ$，$E$ 为 $AC$ 中点，
所以 $AE=DE=CE=\dfrac 12AC$，
同理可证 $AE=NE=CE=\dfrac 12AC$，
所以 $AE=NE=CE=DE$，
所以 $A,N,D,C$ 在以点 $E$ 为圆心，$AC$ 为直径的圆上，
所以 $\angle DEP=2\angle MAD$，
所以 $\angle APE=2\angle MAD$．
因为 $AB=AC$，$AD$ 为 $BC$ 边上的高，所以 $D$ 为 $BC$ 中点，
因为 $E$ 为 $AC$ 中点，
所以 $ED\parallel AB$，
所以 $\angle DEP=\angle APE$，
因为 $\angle ADC=90^\circ$，$E$ 为 $AC$ 中点，
所以 $AE=DE=CE=\dfrac 12AC$，
同理可证 $AE=NE=CE=\dfrac 12AC$，
所以 $AE=NE=CE=DE$，
所以 $A,N,D,C$ 在以点 $E$ 为圆心，$AC$ 为直径的圆上，
所以 $\angle DEP=2\angle MAD$，
所以 $\angle APE=2\angle MAD$．
答案
解析
备注
