如图，在 $\triangle ABC$ 中，过点 $A$ 作 $AD\perp BC$ 于点 $D$，过点 $D$ 作 $AB,AC$ 的垂线，垂足分别为点 $E,F$，求证：$B,E,F,C$ 四点共圆．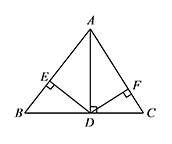
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
因为 $DF\perp AC$，$DE\perp AB$，
所以 $\angle AED+\angle AFD=180^\circ$，即 $A,E,D,F$ 四点共圆．
连接 $EF$，则 $\angle AEF=\angle ADF$．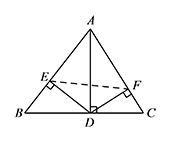
因为 $AD\perp BC$，$DF\perp AC$，
所以 $\angle FCD=\angle ADF=\angle AEF$，
所以 $B,E,F,C$ 四点共圆．
所以 $\angle AED+\angle AFD=180^\circ$，即 $A,E,D,F$ 四点共圆．
连接 $EF$，则 $\angle AEF=\angle ADF$．
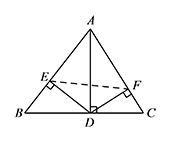因为 $AD\perp BC$，$DF\perp AC$，所以 $\angle FCD=\angle ADF=\angle AEF$，
所以 $B,E,F,C$ 四点共圆．
答案
解析
备注
