如图，$AC,BD$ 是四边形 $ABCD$ 的对角线，若 $\angle ACB=\angle ACD=\angle ABD=\angle ADB$，当 $\angle ACB=\alpha$ 时，则线段 $BC,CD,AC$ 三者之间有何等量关系？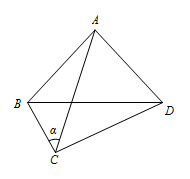
【难度】
【出处】
无
【标注】
【答案】
$BD+CD=2AC\cos \alpha$
【解析】
因为 $\angle ACB=\angle ACD=\angle ABD=\angle ADB$，
所以 $A,B,C,D$ 四点共圆，所以 $\angle ABC+\angle ADC=180^\circ$．
将 $\triangle ABC$ 绕点 $A$ 旋转，使得点 $B$ 与点 $D$ 重合．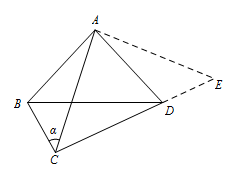
所以 $C,D,E$ 三点共线，
因为 $AC=AE,BC=DE$，所以 $\cos\angle E=\dfrac{\dfrac12(CD+DE)}{AE}$，
所以 $BD+CD=2AC\cos \alpha$．
所以 $A,B,C,D$ 四点共圆，所以 $\angle ABC+\angle ADC=180^\circ$．
将 $\triangle ABC$ 绕点 $A$ 旋转，使得点 $B$ 与点 $D$ 重合．
所以 $C,D,E$ 三点共线，因为 $AC=AE,BC=DE$，所以 $\cos\angle E=\dfrac{\dfrac12(CD+DE)}{AE}$，
所以 $BD+CD=2AC\cos \alpha$．
答案
解析
备注
