在 $\mathrm {Rt}\triangle ABC$ 中,$\angle BAC=90^\circ$,过点 $B$ 的直线 $MN\parallel AC$,$D$ 为 $BC$ 边上一点,连接 $AD$,作 $DE\perp AD$ 交 $MN$ 于点 $E$,连接 $AE$.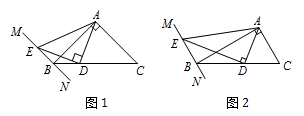

【难度】
【出处】
无
【标注】
-
如图 1,当 $\angle ABC=45^\circ$ 时,求证:$AD=DE$;标注答案略解析因为 $\angle BAC=90^\circ$,$MN\parallel AC$,
所以 $\angle ABE=\angle BAC=90^\circ$.
而 $\angle ADE=90^\circ$,
所以 $A,D,B,E$ 四点共圆,
所以 $\angle AED=\angle ABD=45^\circ$,
所以 $AD=DE$. -
如图 2,当 $\angle ABC=30^\circ$ 时,线段 $AD$ 与 $DE$ 有何数量关系?并请说明理由;标注答案$AD=\dfrac{\sqrt 3}3DE$解析同第1问可得 $\angle AED=\angle ABD=30^\circ$,
所以 $\dfrac{AD}{DE}=\tan 30^\circ=\dfrac{\sqrt 3}3$,
即 $AD=\dfrac{\sqrt 3}3DE$, -
当 $\angle ABC=\alpha$ 时,请直接写出线段 $AD$ 与 $DE$ 的数量关系.(用含 $\alpha$ 的三角函数表示)标注答案$AD=DE\cdot\tan\alpha$解析同第1问可得 $\angle AED=\angle ABD=\alpha$,
所以 $\dfrac{AD}{DE}=\tan \alpha$,
即 $AD=DE\cdot\tan\alpha$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3