若四边形 $ABCD$ 中，$AD\parallel BC$，$\angle CAD=90^\circ $，点 $E$ 在边 $AB$ 上，$CE\perp DE$．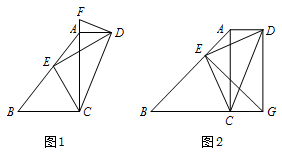
【难度】
【出处】
无
【标注】
-
作 $\angle ADF=\angle AED$，交 $CA$ 的延长线于点 $F$（如图1），求证：$DF$ 为 $\mathrm {Rt}\triangle ACD$ 的外接圆的切线；标注答案略解析如图，以 $CD$ 为直径作 $\odot O$，则 $\odot O$ 为 $\mathrm {Rt}\triangle ACD$ 的外接圆．
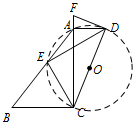因为 $\angle DAC=\angle DEC=90^\circ$，
所以点 $E$ 在 $\odot O$ 上，
所以 $\angle ACD=\angle AED$．
因为 $\angle FDA=\angle AED$，
所以 $\angle ACD=\angle FDA$．
因为 $\angle DAC=90^\circ$，
所以 $\angle ACD+\angle ADC=90^\circ$，
所以 $\angle FDA+\angle ADC=90^\circ$，
所以 $OD\perp DF$，
所以 $DF$ 为 $\mathrm {Rt}\triangle ACD$ 的外接圆的切线． -
如图2，点 $G$ 在 $BC$ 的延长线上，$\angle BGE=\angle BAC$，已知 $\sin \angle AED=\dfrac 25$，$AD=1$，求 $DG$ 的长．标注答案$DG=\dfrac {\sqrt {21}}{2}$解析因为 $\angle BGE=\angle BAC$，
所以 $C,G,A,E$ 四点共圆．
而 $C,A,E$ 三点在 $\mathrm {Rt}\triangle ACD$ 的外接圆 $\odot O$ 上，
所以点 $G$ 在 $\odot O$ 上．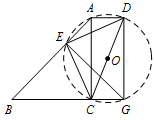
因为 $CD$ 是直径，
所以 $\angle DGC=90^\circ$．
因为 $AD \parallel BC$，
所以 $\angle ADG=90^\circ$．
因为 $\angle DAC=90^\circ$，
所以四边形 $ACGD$ 为矩形，
所以 $DG=AC$．
因为 $\sin \angle AED=\dfrac 25$，$\angle ACD=\angle AED$，
所以 $\sin \angle ACD=\dfrac 25$．
在 $\mathrm {Rt}\triangle ACD$ 中，$AD=1$，$\sin \angle ACD=\dfrac 25$，
则 $CD=\dfrac 52$，$AC=\dfrac {\sqrt {21}}{2}$，
所以 $DG=\dfrac {\sqrt {21}}{2}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
