如图，已知二次函数的图象 $M$ 经过 $A\left(-1,0\right)$，$B\left(4,0\right)$，$C\left(2,-6\right)$ 三点．
【难度】
【出处】
无
【标注】
-
点 $G$ 是线段 $AC$ 上的动点（点 $ G $ 与线段 $ AC $ 的端点不重合），若 $\triangle ABG$ 与 $\triangle ABC$ 相似，求点 $G$ 的坐标；标注答案点 $G$ 的坐标为 $\left(\dfrac 23,-\dfrac {10}{3}\right)$解析因为二次函数的图象 $ M $ 经过 $A\left(-1,0\right)$，$B\left(4,0\right)$ 两点，
所以可设二次函数的解析式为 $y=a\left(x+1\right)\left(x-4\right)$．
因为二次函数的图象 $M$ 经过 $C\left(2,-6\right)$ 点，
所以 $-6=a\left(2+1\right)\left(2-4\right)$，解得 $a=1$．
所以二次函数的解析式为 $y=\left(x+1\right)\left(x-4\right)$，即 $y=x^2-3x-4$．
设直线 $AC$ 的解析式为 $y=sx+t$，把 $A$，$C$ 坐标代入可得
$\begin{cases} 0=-s+t, \\ -6=2s+t,\end{cases}$ 解得 $\begin{cases}s=-2, \\ t=-2.\end{cases}$
所以直线 $AC$ 的解析式为 $y=-2x-2$，
设点 $G$ 的坐标为 $\left(k,-2k-2\right)$．
因为 $ G$ 与 $C$ 点不重合，
所以 $\triangle ABG$ 与 $\triangle ABC$ 相似只有 $\triangle AGB\backsim \triangle ABC$ 一种情况．
所以 $\dfrac {AG}{AB}=\dfrac {AB}{AC}$．
因为 $ AB=5$，$AC=\sqrt {\left[2-\left(-1\right)\right]^2+\left(-6-0\right)^2}=3\sqrt 5$，$AG=\sqrt {\left(k+1\right)^2+\left(-2k-2\right)^2}=\sqrt 5 \left|k+1 \right|$，
所以 $ \dfrac {\sqrt 5 \left|k+1 \right|}{5}=\dfrac {5}{3\sqrt 5}$，
所以 $\left|k+1 \right|=\dfrac 53$，
所以 $ k=\dfrac 23$ 或 $k=-\dfrac 83$（舍去），
所以点 $G$ 的坐标为 $\left(\dfrac 23,-\dfrac {10}{3}\right)$． -
设图象 $M$ 的对称轴为 $l$，点 $D\left(m,n\right)\left(- 1 < m < 2\right)$ 是图象 $M$ 上一动点，当 $\triangle ACD$ 的面积为 $\dfrac{27}{8}$ 时，点 $D$ 关于 $l$ 的对称点为 $E$，能否在图象 $M$ 和 $l$ 上分别找到点 $P$，$Q$，使得以点 $D$，$E$，$P$，$Q$ 为顶点的四边形为平行四边形．若能，求出点 $P$ 的坐标；若不能，请说明理由．标注答案能．$P\left(\dfrac 32 ,-\dfrac{25}{4}\right)$解析
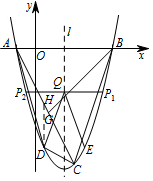如图，过 $D$ 点作 $ x $ 轴的垂线交 $ AC $ 于点 $ H $，
因为 $D\left(m,n\right)\left(-1<m<2\right) $，
所以 $ H\left(m,-2m-2\right)$．
因为点 $D\left(m,n\right)$ 在图象 $M$ 上，
所以 $ D\left(m,m^2-3m-4\right)$．
因为 $\triangle ACD$ 的面积为 $\dfrac {27}{8}$，
所以 $\dfrac 12\left[-2m-2-\left(m^2-3m-4\right)\right]\left[\left(m+1\right)+\left(2-m\right)\right]=\dfrac {27}{8}$，即 $4m^2-4m+1=0$，解得 $m=\dfrac 12$．
所以 $ D\left(\dfrac 12,-\dfrac {21}{4}\right)$．
因为 $y=x^2-3x-4=\left(x-\dfrac 32\right)^2-\dfrac {25}{4}$，
所以图象 $ M $ 的对称轴 $ l $ 为 $x=\dfrac 32$．
因为点 $D$ 关于 $l$ 的对称点为 $E$，
所以 $E\left(\dfrac 52,-\dfrac {21}{4}\right)$，
所以 $DE=\dfrac 52-\dfrac 12=2$，
若以点 $D$，$E$，$P$，$Q$ 为顶点的四边形为平行四边形，
① 以 $DE$ 为底，$PQ\parallel DE$ 且 $PQ=DE=2$．
所以点 $P$ 的横坐标为 $\dfrac 32+2=\dfrac 72$ 或 $\dfrac 32-2=-\dfrac 12$，
所以点 $P$ 的纵坐标为 $\left(\dfrac 72-\dfrac 32\right)^2-\dfrac {25}{4}=-\dfrac 94$，
所以点 $P$ 的坐标为 $\left(\dfrac 72,-\dfrac 94\right)$ 或 $\left(-\dfrac 12,-\dfrac 94\right)$．
② 以 $DE$ 为对角线，$PQ$ 过 $DE$ 中点，
所以 $P$ 为抛物线顶点，$P\left(\dfrac 32 ,-\dfrac{25}{4}\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
