已知抛物线 $y=-x^2+mx-n$ 的对称轴为 $x=-2$，且与 $x$ 轴只有一个交点．
【难度】
【出处】
无
【标注】
-
求 $m,n$ 的值；标注答案$m=-4$，$n=4$解析由抛物线的对称轴为 $x=-2$，可得 $m=-4$．
因为抛物线与 $x$ 轴只有一个交点，
所以 $\Delta =m^2-4n=0$，
从而 $n=4$． -
把抛物线沿 $x$ 轴翻折，再向右平移 $2$ 个单位，向下平移 $1$ 个单位，得到新的抛物线 $C$，求新抛物线 $C$ 的解析式；标注答案抛物线 $C$ 的解析式为 $y=x^2-1$解析原抛物线的解析式为 $y=-x^2-4x-4=-\left(x+2\right)^2$，
所以抛物线 $C$ 的解析式为 $y=x^2-1$． -
已知 $P$ 是 $y$ 轴上的一动点，点 $B$ 的坐标为 $\left(0,1\right)$，问：在抛物线 $C$ 上是否存在点 $D$，使 $\triangle BPD$ 为等边三角形？若存在，请求出 $D$ 的坐标；若不存在，请说明理由．标注答案存在，点 $D$ 的坐标为 $\left(\sqrt 3,2\right),\left(-\sqrt 3,2\right),\left(\dfrac {2\sqrt 3}3,\dfrac 13\right),\left(-\dfrac {2\sqrt 3}3,\dfrac 13\right)$解析假设点 $D$ 存在，设 $D\left(d,d^2-1\right)$．
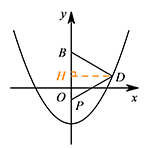如图，作 $DH\perp y$ 轴于点 $H$，则 $DH^2=d^2$，$BH^2=\left(d^2-2\right)^2$．
若 $\triangle DHB$ 是等边三角形，则有 $\dfrac {DH}{BH}=\sqrt 3$，
即 $d^2=3\left(d^2-2\right)^2$，
解得 $d_1=\pm {\sqrt 3}$，$d_2=\pm {\dfrac {2\sqrt 3}{3}}$．
所以满足条件的点 $D$ 的坐标为 $\left(\sqrt 3,2\right),\left(-\sqrt 3,2\right),\left(\dfrac {2\sqrt 3}3,\dfrac 13\right),\left(-\dfrac {2\sqrt 3}3,\dfrac 13\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
