如图,在平面直角坐标系中,抛物线 $y=-\dfrac 13x^2+\dfrac{2\sqrt 3}{3}x+3$ 与 $x$ 轴交于 $A,B$ 两点(点 $A$ 在点 $B$ 的左侧),与 $y$ 轴交于点 $C$,抛物线的顶点为点 $E$.平移抛物线,使抛物线的顶点 $E$ 在射线 $AE$ 上移动,点 $E$ 平移后的对应点为点 $E'$,点 $A$ 的对应点为 $A'$.将 $\triangle AOC$ 绕点 $O$ 顺时针旋转至 $\triangle A_1OC_1$ 的位置,点 $A,C$ 的对应点分别为点 $A_1,C_1$,且点 $A_1$ 恰好落在 $AC$ 上,连接 $C_1A',C_1E'$.$\triangle A'C_1E'$ 是否能为等腰三角形?若能,请求出所有符合条件的点 $E'$ 的坐标;若不能,请说明理由.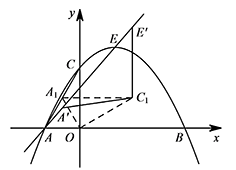
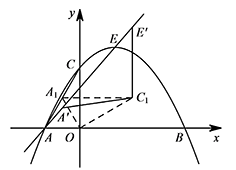
【难度】
【出处】
无
【标注】
【答案】
$\triangle A'C_1E'$ 能为等腰三角形,符合条件的点 $E'$ 的坐标为 $\left(\dfrac{5\sqrt 3+\sqrt{39}}2,7+\sqrt{13}\right)$,$\left(\dfrac{5\sqrt 3-\sqrt{39}}2,7-\sqrt{13}\right)$,$\left(\dfrac{3\sqrt 3}2,5\right)$ 或 $\left(\dfrac{\sqrt 3+\sqrt{39}}2,3+\sqrt{13}\right)$
【解析】
由抛物线解析式求得点 $A(-\sqrt 3,0),C(0,3)$,
所以 $\angle CAO=60^\circ$,$\angle AOA_1=60^\circ$.
由旋转的性质可得 $\angle COC_1=\angle AOA_1=60^\circ$,$OC_1=OC=3$,
所以点 $C_1$ 的坐标为 $\left(\dfrac{3\sqrt 3}2,\dfrac 32\right)$.
易求抛物线的顶点 $E$ 的坐标为 $(\sqrt 3,4)$,
所以直线 $AE$ 的解析式为 $y=\dfrac {2\sqrt 3}3x+2$.
可设点 $A'$ 的坐标为 $\left(t,\dfrac {2\sqrt 3}3t+2\right)$,
则由平移的性质可得 $E'\left(t+2\sqrt 3,\dfrac {2\sqrt 3}3t+6\right)$ 且 $t>-3\sqrt 3$.
所以 $A'E'^2=AE^2=28$,$A'C_1^2=\dfrac 73t^2-\dfrac{7\sqrt 3}3t+7$,$E'C_1^2=\dfrac 73t^2+7\sqrt 3t+21$.
$\triangle A'C_1E'$ 为等腰三角形有三种可能:
① 当 $A'E'=A'C_1$ 时,有 $\dfrac 73t^2-\dfrac{7\sqrt 3}3t+7=28$,
解得 $t=\dfrac{\sqrt 3\pm \sqrt{39}}2$,
此时点 $E'$ 的坐标为 $\left(\dfrac{5\sqrt 3+\sqrt{39}}2,7+\sqrt{13}\right)$ 或 $\left(\dfrac{5\sqrt 3-\sqrt{39}}2,7-\sqrt{13}\right)$;
② 当 $A'C_1=E'C_1$ 时,有 $\dfrac 73t^2-\dfrac{7\sqrt 3}3t+7=\dfrac 73t^2+7\sqrt 3t+21$,
解得 $t=-\dfrac{\sqrt 3}2$,
此时点 $E'$ 的坐标为 $\left(\dfrac{3\sqrt 3}2,5\right)$;
③ 当 $A'E'=C_1E'$ 时,有 $\dfrac 73t^2+7\sqrt 3t+21=28$,
解得 $t=\dfrac{-3\sqrt 3\pm \sqrt{39}}2$,
而 $t>-3\sqrt 3$,所以 $t=\dfrac{-3\sqrt 3+\sqrt{39}}2$,
此时点 $E'$ 的坐标为 $\left(\dfrac{\sqrt 3+\sqrt{39}}2,3+\sqrt{13}\right)$.
综上可得,符合条件的点 $E'$ 的坐标为 $\left(\dfrac{5\sqrt 3+\sqrt{39}}2,7+\sqrt{13}\right)$,$\left(\dfrac{5\sqrt 3-\sqrt{39}}2,7-\sqrt{13}\right)$,$\left(\dfrac{3\sqrt 3}2,5\right)$ 或 $\left(\dfrac{\sqrt 3+\sqrt{39}}2,3+\sqrt{13}\right)$.
所以 $\angle CAO=60^\circ$,$\angle AOA_1=60^\circ$.
由旋转的性质可得 $\angle COC_1=\angle AOA_1=60^\circ$,$OC_1=OC=3$,
所以点 $C_1$ 的坐标为 $\left(\dfrac{3\sqrt 3}2,\dfrac 32\right)$.
易求抛物线的顶点 $E$ 的坐标为 $(\sqrt 3,4)$,
所以直线 $AE$ 的解析式为 $y=\dfrac {2\sqrt 3}3x+2$.
可设点 $A'$ 的坐标为 $\left(t,\dfrac {2\sqrt 3}3t+2\right)$,
则由平移的性质可得 $E'\left(t+2\sqrt 3,\dfrac {2\sqrt 3}3t+6\right)$ 且 $t>-3\sqrt 3$.
所以 $A'E'^2=AE^2=28$,$A'C_1^2=\dfrac 73t^2-\dfrac{7\sqrt 3}3t+7$,$E'C_1^2=\dfrac 73t^2+7\sqrt 3t+21$.
$\triangle A'C_1E'$ 为等腰三角形有三种可能:
① 当 $A'E'=A'C_1$ 时,有 $\dfrac 73t^2-\dfrac{7\sqrt 3}3t+7=28$,
解得 $t=\dfrac{\sqrt 3\pm \sqrt{39}}2$,
此时点 $E'$ 的坐标为 $\left(\dfrac{5\sqrt 3+\sqrt{39}}2,7+\sqrt{13}\right)$ 或 $\left(\dfrac{5\sqrt 3-\sqrt{39}}2,7-\sqrt{13}\right)$;
② 当 $A'C_1=E'C_1$ 时,有 $\dfrac 73t^2-\dfrac{7\sqrt 3}3t+7=\dfrac 73t^2+7\sqrt 3t+21$,
解得 $t=-\dfrac{\sqrt 3}2$,
此时点 $E'$ 的坐标为 $\left(\dfrac{3\sqrt 3}2,5\right)$;
③ 当 $A'E'=C_1E'$ 时,有 $\dfrac 73t^2+7\sqrt 3t+21=28$,
解得 $t=\dfrac{-3\sqrt 3\pm \sqrt{39}}2$,
而 $t>-3\sqrt 3$,所以 $t=\dfrac{-3\sqrt 3+\sqrt{39}}2$,
此时点 $E'$ 的坐标为 $\left(\dfrac{\sqrt 3+\sqrt{39}}2,3+\sqrt{13}\right)$.
综上可得,符合条件的点 $E'$ 的坐标为 $\left(\dfrac{5\sqrt 3+\sqrt{39}}2,7+\sqrt{13}\right)$,$\left(\dfrac{5\sqrt 3-\sqrt{39}}2,7-\sqrt{13}\right)$,$\left(\dfrac{3\sqrt 3}2,5\right)$ 或 $\left(\dfrac{\sqrt 3+\sqrt{39}}2,3+\sqrt{13}\right)$.
答案
解析
备注