如图,反比例函数 $y=\dfrac{k}{x}$ 的图象与一次函数 $y=\dfrac{1}{4}x$ 的图象交于点 $A,B$,点 $B$ 的横坐标是 $4$.点 $P$ 是第一象限内反比例函数图象上的动点,且在直线 $AB$ 的上方.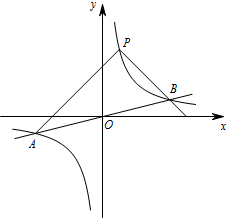

【难度】
【出处】
无
【标注】
-
若点 $P$ 的坐标是 $\left(1,4\right)$,直接写出 $k$ 的值和 $\triangle PAB$ 的面积;标注答案$k=4$,$\triangle PAB$ 的面积为 $15$解析如图,过点 $A$ 作 $AR\perp y$ 轴于 $R$,过点 $P$ 作 $PS\perp y$ 轴于 $S$,连接 $PO$,令 $AP$ 与 $y$ 轴交于点 $C$.
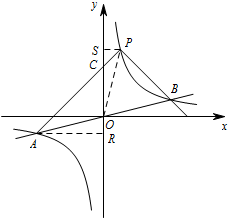 把 $x=4$ 代入 $y=\dfrac14x$,得到点 $B$ 的坐标为 $(4,1)$,
把 $x=4$ 代入 $y=\dfrac14x$,得到点 $B$ 的坐标为 $(4,1)$,
把点 $D\left(4,1\right)$ 代入 $y=\dfrac kx$ 得 $k=4$.
解方程组 $\begin{cases}y=\dfrac14x,\\y=\dfrac4x,\end{cases}$ 得到点 $A$ 的坐标为 $\left(-4,-1\right)$,
则点 $A$ 与点 $B$ 关于原点对称,即 $OA=OB$.
$\therefore S_{\triangle PAB}=2S_{\triangle AOP}=2S_{\triangle BOP}$.
设直线 $AP$ 的解析式为 $y=mx+n$.
把点 $A\left(-4,-1\right),P\left(1,4\right)$ 的坐标代入解析式,
求得直线 $AP$ 解析式为 $y=x+3$,
则点 $C$ 的坐标为 $\left(0,3\right)$,$OC=3$.
$\begin{split}\text{所以}S_{\triangle AOP}&=S_{\triangle AOC}+S_{POC}\\&=\dfrac12OC\cdot AR+\dfrac12OC\cdot PS\\&=\dfrac12\times3\times4+\dfrac12\times3\times1\\&=\dfrac{15}{2},\end{split}$
从而 $S_{\triangle PAB}=2S_{\triangle AOP}=15$. -
设直线 $PA,PB$ 与 $x$ 轴分别交于点 $M,N$,求证:$\triangle PMN $ 是等腰三角形;标注答案略解析如图,过点 $P$ 作 $PH\perp x$ 轴.
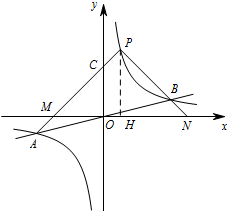 设直线 $PB$ 的解析式为 $y=ax+b$,
设直线 $PB$ 的解析式为 $y=ax+b$,
把点 $P\left(1,4\right),B\left(4,1\right)$ 代入解析式得 $\begin{cases}a+b=4,\\4a+b=1,\end{cases}$
解得 $\begin{cases}a=-1,\\b=5,\end{cases}$
所以直线 $PB$ 的解析式为 $y=-x+5$.
当 $y=0$ 时,得 $x=5$,所以点 $N\left(5,0\right)$.
同理可得点 $M\left(-3,0\right)$.
所以 $MH=1-\left(-3\right)=4$,$NH=5-1=4$,
即 $MH=NH$,
所以 $PH$ 垂直平分 $MN$,
所以 $PM=PN$,
所以 $\triangle PMN$ 是等腰三角形. -
设点 $Q$ 是反比例函数图象上位 于 $P,B$ 之间的动点(与点 $P,B$ 不重合),连接 $AQ,BQ$,比较 $\angle PAQ$ 与 $\angle PBQ$ 的大小,并说明理由.标注答案$\angle PAQ=\angle PBQ$解析如图,过点 $Q$ 作 $QT\perp x$ 轴于点 $T$,设 $AQ$ 交 $x$ 轴于点 $D$,$QB$ 的延长线交 $x$ 轴于点 $E$.
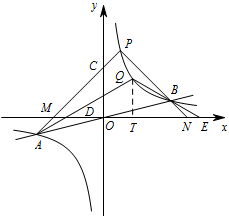 可设点 $Q$ 为 $\left(c,\dfrac4c\right)$,直线 $AQ$ 的解析式为 $y=px+q$,
可设点 $Q$ 为 $\left(c,\dfrac4c\right)$,直线 $AQ$ 的解析式为 $y=px+q$,
则有 $\begin{cases}-4p+q=-1,\\cp+q=\dfrac4c,\end{cases}$ 解得 $\begin{cases}p=\dfrac1c,\\q=\dfrac4c-1.\end{cases}$
所以直线 $AQ$ 的解析式为 $y=\dfrac1cx+\dfrac4c-1$.
当 $y=0$ 时,$\dfrac1cx+\dfrac4c-1=0$,解得 $x=c-4$,
所以点 $D\left(c-4,0\right)$.
同理可得 $E\left(c+4,0\right)$,
所以 $DT=c-\left(c-4\right)=4$,$ET=c+4-c=4$,
所以 $DT=ET$,
所以 $QT$ 垂直平分 $DE$,
所以 $QD=QE$,
所以 $\angle QDE=\angle QED$.
因为 $\angle MDA=\angle QDE$,
所以 $\angle MDA=\angle QED$.
因为 $PM=PN $,
所以 $\angle PMN=\angle PNM$.
因为 $\angle PAQ=\angle PMN-\angle MDA$,$\angle PBQ=\angle NBE=\angle PNM-\angle QED$,
所以 $\angle PAQ=\angle PBQ$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3