如图,抛物线 $y=x^2+bx+c$ 与 $x$ 轴交于 $A、B$ 两点,$B$ 点坐标为 $\left(3,0\right)$,与 $y$ 轴交于点 $C\left(0,-3\right)$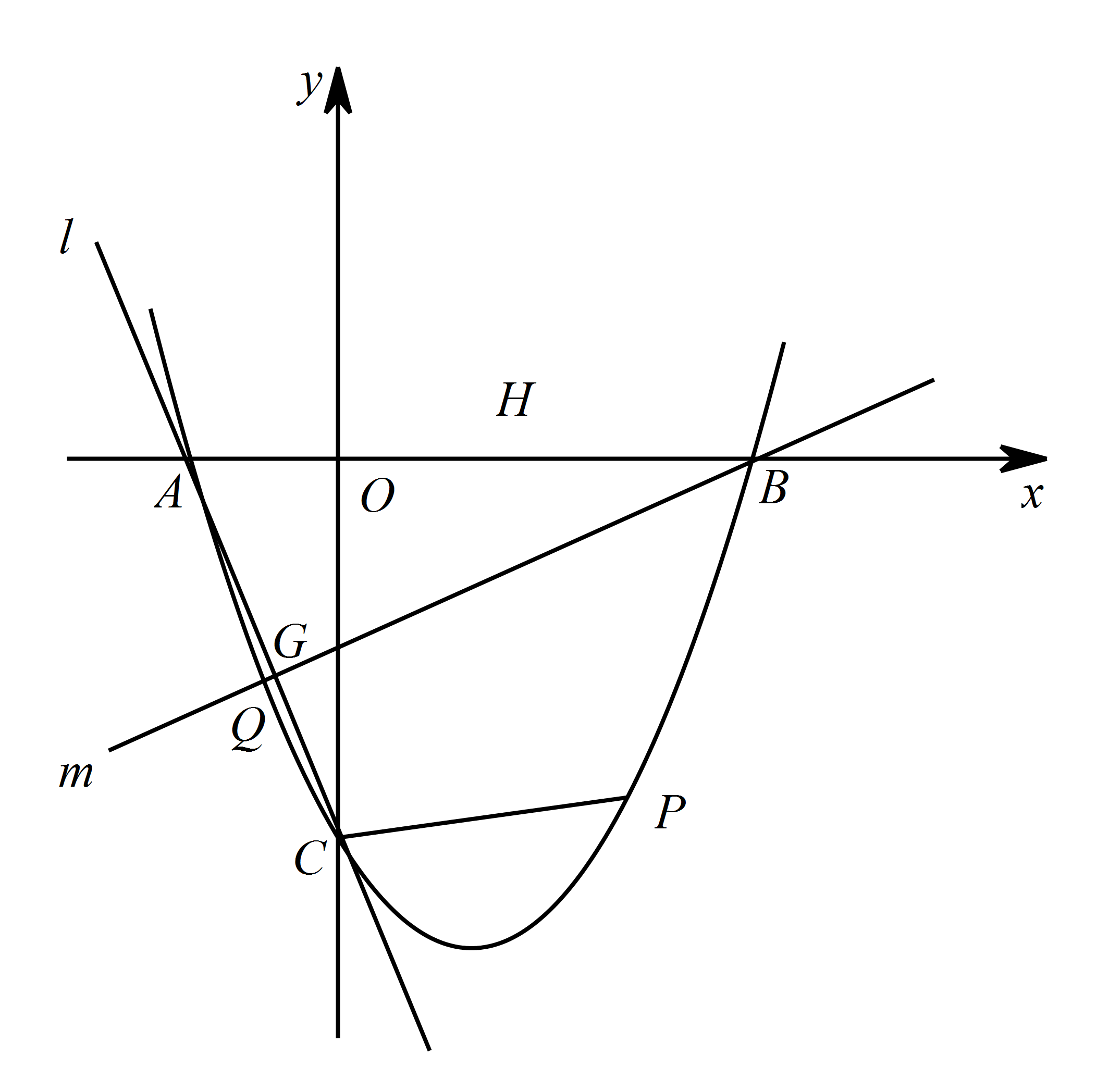

【难度】
【出处】
无
【标注】
-
点 $ P $ 在抛物线位于第四象限的部分上运动,当四边形 $ ABPC $ 的面积最大时,求点 $ P $ 的坐标和四边形 $ ABPC $ 的最大面积.标注答案当 $P$ 点坐标为 $\left(\dfrac{3}{2},-\dfrac{15}{4}\right)$ 时,四边形 $ABPC$ 的面积最大,最大面积为 $\dfrac{75}{8}$解析把 $B、C$ 两点坐标代入抛物线解析式可得
$\begin{cases}9+3b+c=0,\\c=-3,\end{cases}$ 解得 $\begin{cases}b=-2,\\c=-3,\end{cases}$
所以抛物线解析式为 $y=x^2-2x-3$.
如图,连接 $BC$,过 $P$ 做 $ y $ 轴的平行线,交 $BC$ 于点 $M$,交 $x$ 轴于点 $H$,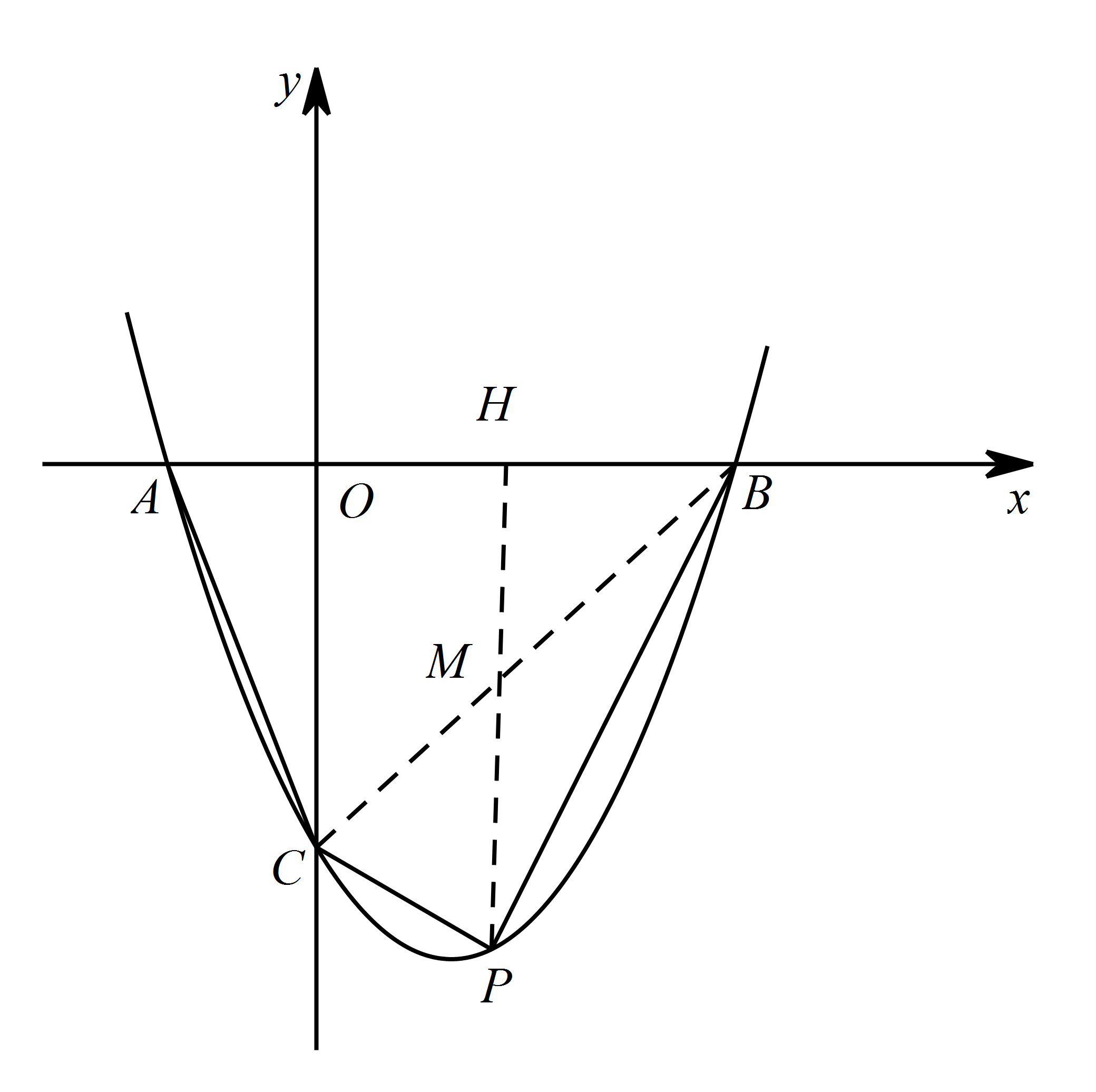 在 $y=x^2-2x-3$ 中,令 $y=0$ 可得 $0=x^2-2x-3$,
在 $y=x^2-2x-3$ 中,令 $y=0$ 可得 $0=x^2-2x-3$,
解得 $x=-1或x=3$.
所以 $A$ 点坐标为 $\left(-1,0\right)$,
所以 $AB=3-\left(-1\right)=4$,且 $OC=3$,
所以
$\begin{split} S_{\triangle ABC} &=\dfrac{1}{2}AB\cdot OC\\ &=\dfrac{1}{2}\times 4\times 3\\ &=6.\end{split}$
因为 $B$ $\left(3,0\right)$,$C$ $\left(0,-3\right)$,
所以直线 $BC$ 解析式为 $y=x-3$.
设 $P$ 点坐标为 $\left(x,x^2-2x-3\right)$,则 $M$ 点坐标为 $\left(x,x-3\right)$,
因为 $P$ 点在第四限,
所以 $PM=x-3-\left(x^2-2x-3\right)=-x^2+3x$,
所以
$\begin{split}S_{\triangle PBC}&=\dfrac{1}{2}PM\cdot OH+\dfrac{1}{2}PM\cdot HB\\ &=\dfrac{1}{2}PM\cdot \left(OH+HB\right)\\ &=\dfrac{1}{2}PM\cdot OB\\ &=\dfrac{1}{2}PM,\end{split}$
所以当 $PM$ 有最大值时,
$\triangle PBC$ 的面积最大,则四边形 $ABPC$ 的面积最大.
因为 $PM=-x^2+3x=-\left(x-\dfrac{3}{2}\right)^2+\dfrac{9}{4}$,
所以当 $x=\dfrac{3}{2}$ 时,$PM_{max}=\dfrac{9}{4}$.则 $S_{\triangle PBC}=\dfrac{3}{2}\times \dfrac{9}{4}=\dfrac{27}{8}$,
此时 $P$ 点坐标为 $\left(\dfrac{3}{2},-\dfrac{15}{4}\right)$.
则 $S_{四边形ABPC}=S_{\triangle ABC}+S_{\triangle PBC}=6+\dfrac{27}{8}=\dfrac{75}{8}$,
即当 $P$ 点坐标为 $\left(\dfrac{3}{2},-\dfrac{15}{4}\right)$ 时,四边形 $ABPC$ 的面积最大,最大面积为 $\dfrac{75}{8}$. -
直线 $l$ 经过 $A、C$ 两点,点 $Q$ 在抛物线位于 $y$ 轴左侧的部分上运动,直线 $m$ 经过点 $B$ 和点 $Q$,是否存在直线 $m$,使得直线 $l$、$m$ 与 $x$ 轴围成的三角形和直线 $l$、$m$ 与 $y$ 轴围成的三角形相似?若存在,求出直线 $m$ 的解析式,若不存在,请说明理由.标注答案直线 $m$ 解析式为 $y=\dfrac{1}{3}x-1$解析如图,设直线 $m$ 交 $y$ 轴于点 $N$,交直线 $l$ 于点 $G$,
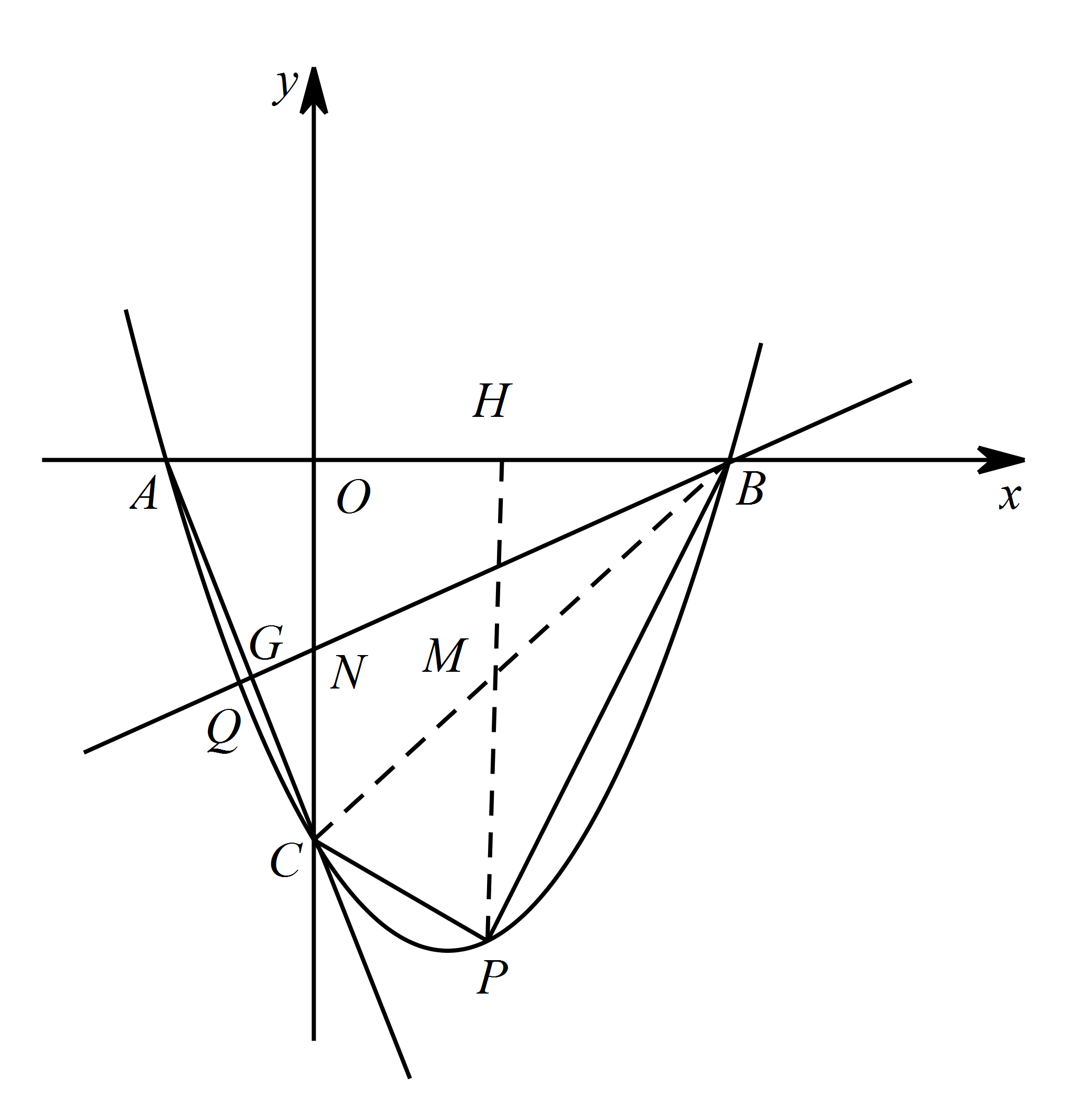 则 $\angle AGP=\angle GNC+\angle GCN$.
则 $\angle AGP=\angle GNC+\angle GCN$.
当 $\triangle AGB$ 和 $\triangle NGC$ 相似时,必有 $\angle AGB=\angle CGB$.
又因为 $\angle AGB+\angle CGB=180^\circ$,
所以 $\angle AGB=\angle CGB=90^\circ$,
所以 $\angle ACO=\angle OBN$.
在 $\mathrm {Rt}\triangle AON$ 和 $\mathrm {Rt}\triangle NOB$ 中
$\begin{cases}\angle AOC=\angle NOB\\OC=OB\\ \angle ACO=\angle NBO\end{cases}$
所以 $\mathrm {Rt}\triangle AON\cong \mathrm {Rt}\triangle NOB\left(ASA\right)$,
所以 $ON=OA=1$,
所以 $N$ 点坐标为 $\left(0,-1\right)$.
设直线 $m$ 解析式为 $y=kx+d$,把 $B、N$ 两点坐标代入可得
$\begin{cases}3k+d=0,\\d=-1,\end{cases}$ 解得 $\begin{cases}k=\dfrac{1}{3},\\d=-1,\end{cases}$
所以直线 $m$ 解析式为 $y=\dfrac{1}{3}x-1$,
即存在满足条件的直线 $m$,其解析式为 $y=\dfrac{1}{3}x-1$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2