如图，抛物线 $y=ax^{2}+bx+c$ 经过 $\triangle ABC$ 的三个顶点，与 $y$ 轴相交于 $\left(0, \dfrac{9}{4 }\right)$，点 $A$ 坐标为 $\left(-1,2\right)$，点 $B$ 是点 $A$ 关于 $y$ 轴的对称点，点 $C$ 在 $x$ 轴的正半轴上．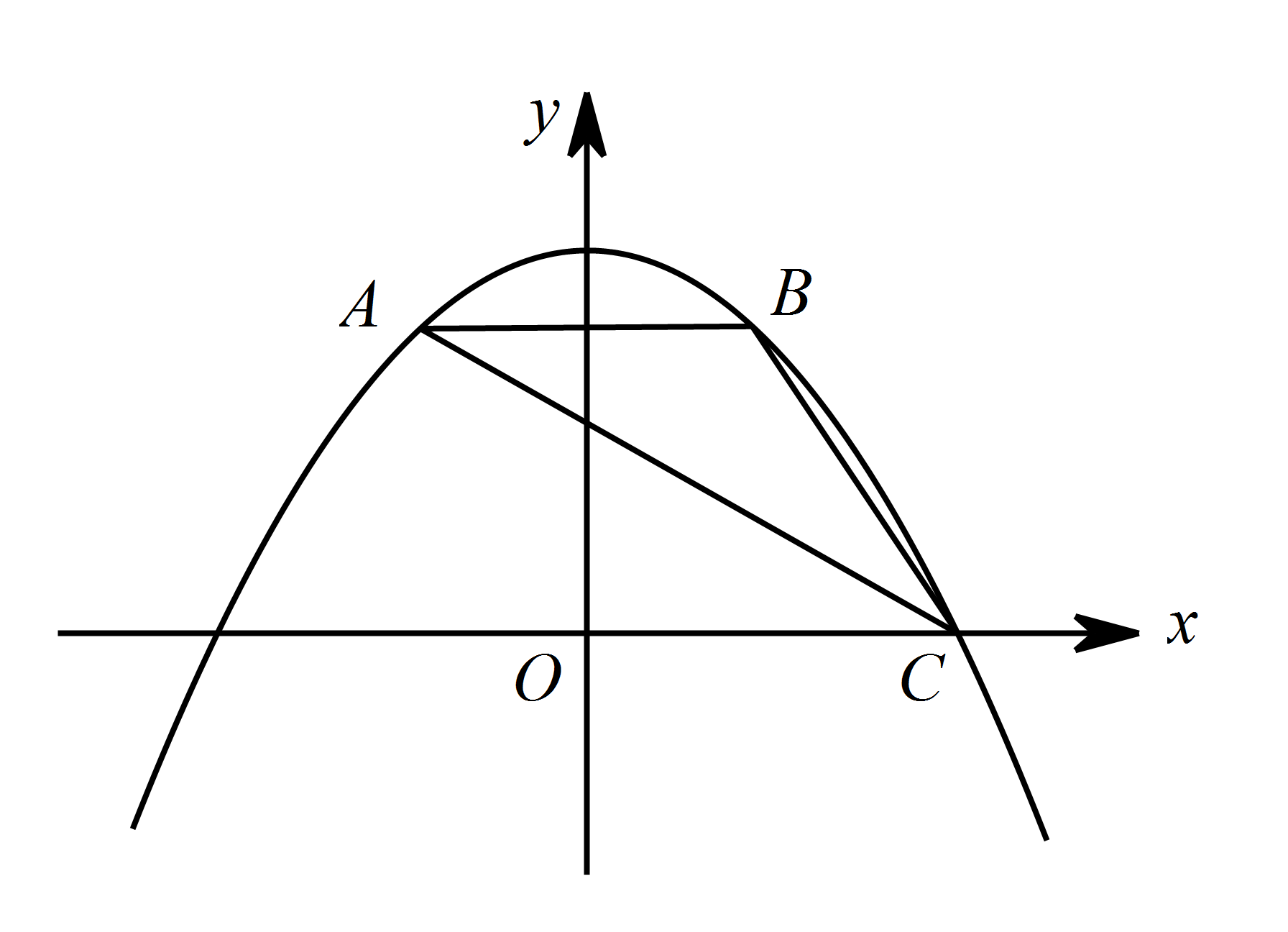
【难度】
【出处】
无
【标注】
-
点 $F$ 为线段 $AC$ 上一动点，过 $F$ 作 $FE\perp x$ 轴，$FG\perp y$ 轴，垂足分别为 $E$，$G$，当四边形 $OEFG$ 为正方形时，求出 $F$ 点的坐标．标注答案点 $F$ 的坐标为 $\left(1,1\right)$解析因为点 $B$ 是点 $A$ 关于 $y$ 轴的对称点，
所以抛物线的对称轴为 $y$ 轴，
所以抛物线的顶点为 $\left(0,\dfrac{9}{ 4}\right)$，
故抛物线的解析式可设为 $y=ax^{2}+\dfrac{9}{4 }$．
因为点 $A\left(-1,2\right)$ 在抛物线 $y=ax^{2}+\dfrac{9}{ 4}$ 上，
所以 $a+\dfrac{9}{ 4}=2$，解得 $a=-\dfrac{1}{4 }$，
所以抛物线的函数关系表达式为 $y=-\dfrac{1}{4 }x^{2}+\dfrac{9}{ 4}$．
① 当点 $F$ 在第一象限时，如图．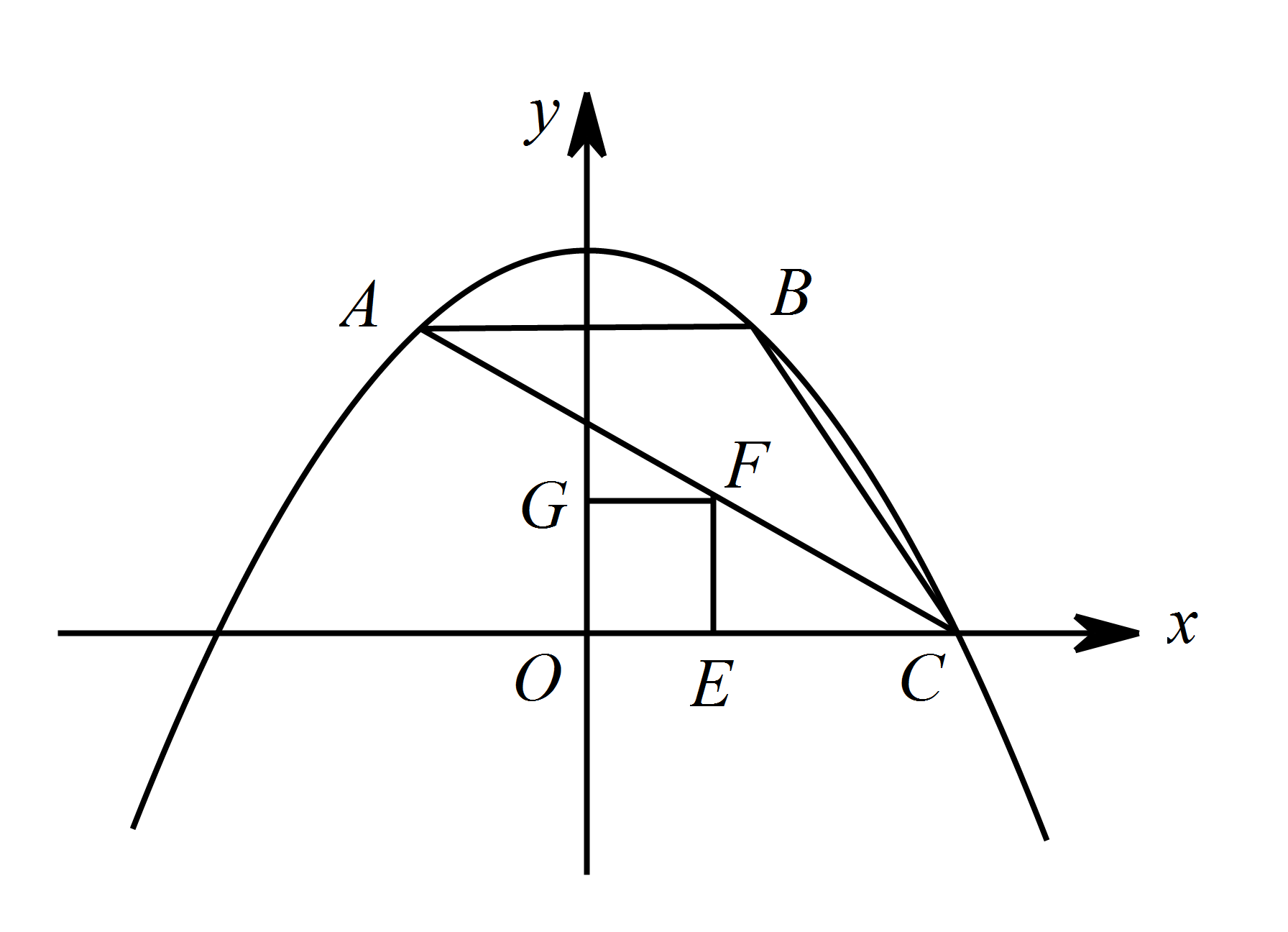
令 $y=0$ 得，$-\dfrac{1}{ 4}x^{2}+\dfrac{9}{ 4}=0$，
解得 $x_{1}=3$，$x_{2}=-3$，
所以点 $C$ 的坐标为 $\left(3,0\right)$．
设直线 $AC$ 的解析式为 $y=mx+n$，
则有 $\begin{cases}-m+n=2,\\3m+n=0,\end{cases}$ 解得 $\begin{cases}m=-\dfrac{1}{ 2},\\n=\dfrac{3}{ 2}.\end{cases}$
所以直线 $AC$ 的解析式为 $y=-\dfrac{1}{ 2}x+\dfrac{3}{ 2}$．
设正方形 $OEFG$ 的边长为 $p$，则点 $F\left(p,p\right)$．
因为点 $F\left(p,p\right)$ 在直线 $y=-\dfrac{1}{ 2}x+\dfrac{3}{2}$ 上，
所以 $-\dfrac{1}{ 2}p+\dfrac{3}{ 2}=p$，解得 $p=1$，
所以点 $F$ 的坐标为 $\left(1,1\right)$．
② 当点 $F$ 在第二象限时，同理可得点 $F$ 的坐标为 $\left(-3,3\right)$，
此时点 $F$ 不在线段 $AC$ 上，故舍去．
综上所述，点 $F$ 的坐标为 $\left(1,1\right)$． -
将第1问中的正方形 $OEFG$ 沿 $OC$ 向右平移，记平移中的正方形 $OEFG$ 为正方形 $DEFG$，当点 $E$ 和点 $C$ 重合时停止运动，设平移的距离为 $t$，正方形的边 $EF$ 与 $AC$ 交于点 $M$，$DG$ 所在的直线与 $AC$ 交于点 $N$，连接 $DM$，是否存在这样的 $t$，使 $\triangle DMN$ 是等腰三角形？若存在，求 $t$ 的值；若不存在请说明理由．标注答案存在，$t$ 的值为 $\dfrac{1}{2}$，$3-\sqrt{5}$ 或 $1$解析过点 $M$ 作 $MH\perp DN$ 于 $H$，如图．
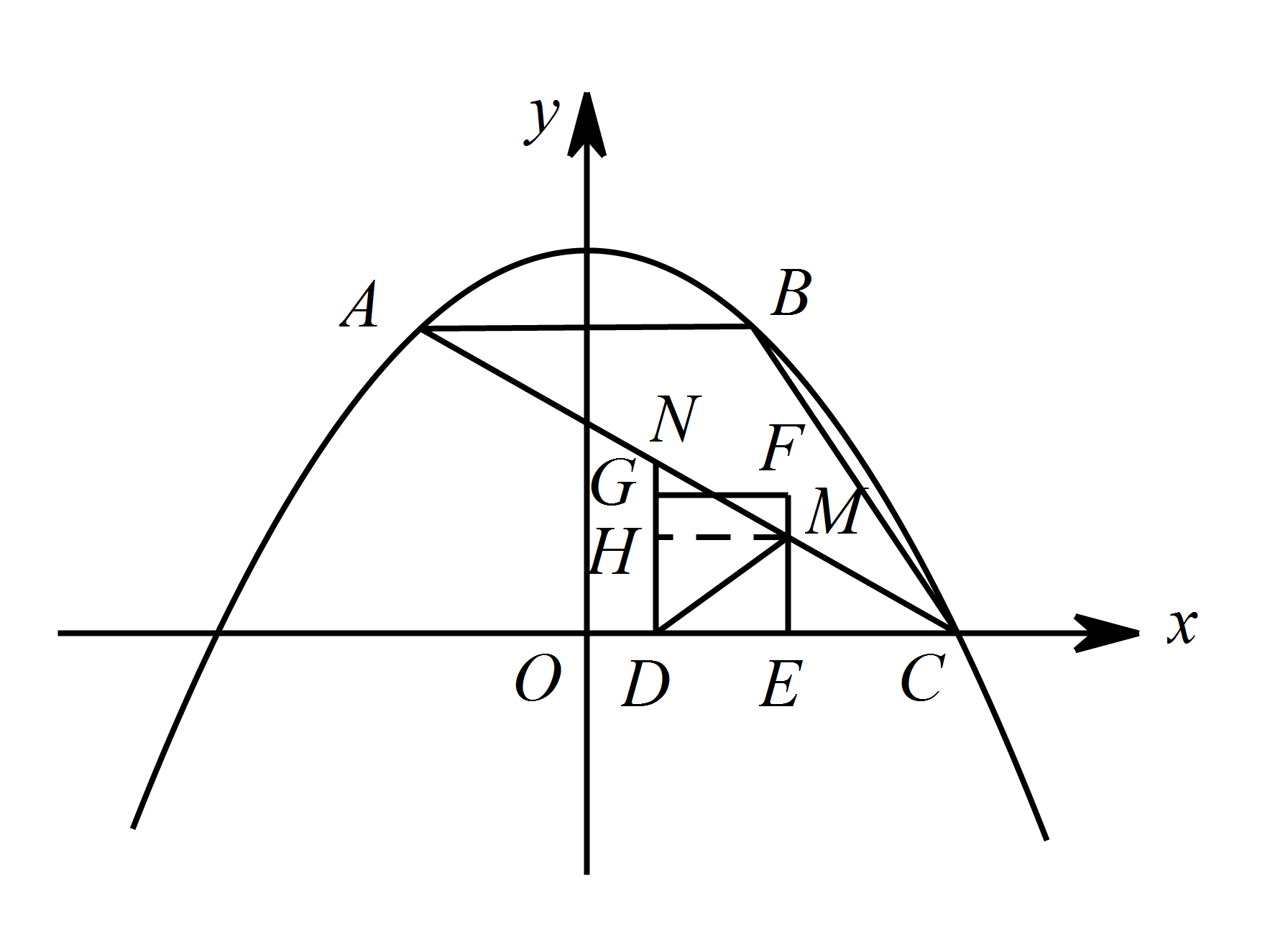则 $OD=t$，$OE=t+1$．
因为点 $E$ 和点 $C$ 重合时停止运动，
所以 $0\leqslant t\leqslant 2$．
当 $x=t$ 时，$y=-\dfrac{1}{2}t+\dfrac{3}{2}$，
则点 $N\left(t,-\dfrac{1}{2}t+\dfrac{3}{2}\right)$，$DN=-\dfrac{1}{2}t+\dfrac{3}{2}$．
当 $x=t+1$ 时，$y=-\dfrac{1}{ 2}\left(t+1\right)+\dfrac{3}{2}=-\dfrac{1}{2}t+1$，
则点 $M\left(t+1,-\dfrac{1}{ 2}t+1\right)$，$ME=-\dfrac{1}{2 }t+1$．
在 $\mathrm {Rt}\triangle DEM$ 中，$DM^{2}=1^{2}+\left(-\dfrac{1}{2}t+1\right)^{2}=\dfrac{1}{ 4}t^{2}-t+2$．
在 $\mathrm {Rt}\triangle NHM$ 中，$MH=1$，$NH=\left(-\dfrac{1}{2}t+\dfrac{3}{2}\right)-\left(-\dfrac{1}{2}t+1\right)=\dfrac{1}{2}$．
所以 $MN^{2}=1^{2}+\left(\dfrac{1}{ 2}\right)^{2}=\dfrac{5}{ 4}$．
① 当 $DN=DM$ 时，有 $\left(-\dfrac{1}{ 2}t+\dfrac{3}{ 2}\right)^{2}=\dfrac{1}{ 2}t^{2}-t+2$，
解得 $t=\dfrac{1}{2}$；
② 当 $ND=NM$ 时，有 $-\dfrac{1}{ 2}t+\dfrac{3}{ 2}=\sqrt{\dfrac{5}{ 4}}=\dfrac{\sqrt{5}}{ 2}$，
解得 $t=3-\sqrt{5}$；
③ 当 $MN=MD$ 时，有 $\dfrac{5}{ 4}=\dfrac{1}{ 4}t^{2}-t+2$，
解得 $t_{1}=1$，$t_{2}=3$．
因为 $0\leqslant t\leqslant 2$，
所以 $t=1$．
综上所述，当 $\triangle DMN$ 是等腰三角形时，$t$ 的值为 $\dfrac{1}{2}$，$3-\sqrt{5}$ 或 $1$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
