如图，抛物线 $ y = a{x^2} + c\left(a \ne 0\right) $ 与 $ y $ 轴交于点 $ A $，与 $ x $ 轴交于点 $ B $，$ C $ 两点（点 $ C $ 在 $ x $ 轴正半轴上），$ \triangle ABC $ 为等腰直角三角形，且面积为 $ 4 $．现将抛物线沿 $ BA $ 方向平移，平移后的抛物线经过点 $ C $ 时，与 $ x $ 轴的另一交点为 $ E $，其顶点为 $ F $，对称轴与 $ x $ 轴的交点为 $ H $．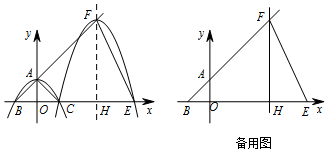
【难度】
【出处】
无
【标注】
-
连接 $ OF $，试判断 $ \triangle OEF $ 是否为等腰三角形，并说明理由；标注答案$\triangle OEF$ 为等腰三角形解析因为 $\triangle ABC$ 为等腰直角三角形，
所以 $OA=\dfrac 12 BC$．
又 $\triangle ABC的面积=\dfrac 12BC\times OA=4$，即 $OA^2=4$，
所以 $OA=2$，
所以点 $A,B,C$ 的坐标分别为 $\left(0,2\right),\left(-2,0\right),\left(2,0\right)$，
从而抛物线的函数表达式为 $y=-\dfrac 12x^2+2$．
连接 $OF$．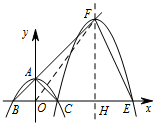
所以直线 $AB$ 的函数表达式为 $ y=x+2 $．
又平移后的抛物线顶点 $F$ 在射线 $ BA $ 上，
所以设顶点 $F$ 的坐标为 $\left(m,m+2\right)$，
所以平移后的抛物线函数表达式为 $y=-\dfrac 12\left(x-m\right)^2+m+2$．
因为抛物线过点 $C\left(2,0\right)$，
所以 $-\dfrac 12\left(2-m\right)^2+m+2=0$，解得 $m_1=0$（舍去），$m_2=6$．
所以平移后的抛物线函数表达式为 $y=-\dfrac 12\left(x-6\right)^2+8$，
即 $y=-\dfrac 12x^2+6x-10$．
当 $y=0$ 时，$-\dfrac 12x^2+6x-10=0$，解得 $x_1=2$，$x_2=10$．
所以点 $E\left(10,0\right)$，$OE=10$，
所以顶点 $F\left(6,8\right)$，$OH=6$，$FH=8$，
所以 $OF=\sqrt{OH^2+FH^2}=\sqrt{6^2+8^2}=10 $，
又 $EF=\sqrt{FH^2+HE^2}=\sqrt{8^2+4^2}=4\sqrt 5 $，
所以 $OE=OF$，即 $\triangle OEF$ 为等腰三角形． -
现将一足够大的三角板的直角顶点 $ Q $ 放在射线 $ AF $ 或射线 $ HF $ 上，一直角边始终过点 $ E $，另一直角边与 $ y $ 轴相交于点 $ P $，是否存在这样的点 $ Q $，使以点 $ P $，$ Q $，$ E $ 为顶点的三角形与 $ \triangle POE $ 全等？若存在，求出点 $ Q $ 的坐标；若不存在，请说明理由．标注答案存在，点 $Q$ 的坐标为 $\left(6,2\sqrt{21}\right)$，$\left(6,3\right)$，$\left(10,12\right)$，$\left(4+\sqrt{14},6+\sqrt{14}\right)$ 或 $\left(4-\sqrt{14},6-\sqrt{14}\right)$解析点 $Q$ 的位置分两种情形：
① 点 $Q$ 在射线 $HF$ 上，当点 $P$ 在 $x$ 轴上方时，如图．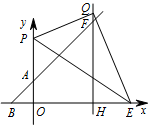
由于 $\triangle PQE\cong\triangle POE$，
所以 $QE=OE=10$．
在 $\mathrm {Rt}\triangle QHE$ 中，$QH=\sqrt{QE^2-HE^2}=\sqrt{10^2-4^2}=2\sqrt{21}$，
所以点 $Q\left(6,2\sqrt{21}\right)$．
当点 $P$ 在 $x$ 轴下方时，如图．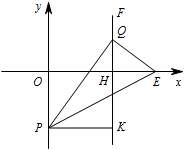
有 $PQ=OE=10$．
过 $P$ 点作 $PK\perp HF$ 于点 $K$，则有 $PK=6$．
在 $\mathrm {Rt}\triangle PQK$ 中，$QK=\sqrt{PQ^2-PK^2}=\sqrt{10^2-6^2}=8$，
因为 $\angle PQE=90^\circ$，
所以 $\angle PQK+\angle HQE=90^\circ$，
因为 $\angle HQE+\angle HEQ=90^\circ$，
所以 $\angle PQK=\angle HEQ$，
又 $\angle PKQ=\angle QHE=90^\circ$，
所以 $\triangle PKQ\backsim\triangle QHE$，
所以 $\dfrac{PK}{QH}=\dfrac{QK}{HE}$，
所以 $\dfrac{6}{QH}=\dfrac 84$，解得 $QH=3$，
所以点 $Q\left(6,3\right)$．
② 点 $Q$ 在射线 $AF$ 上．
当 $PQ=OE=10$ 时，如图．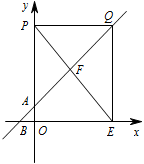
有 $QE=PO$，
所以四边形 $POEQ$ 为矩形，
所以点 $Q$ 的横坐标为 $10$，
当 $x=10$ 时，$y=x+2=12$，
所以点 $Q\left(10,12\right)$．
当 $QE=OE=10$ 时，如图1．
过点 $Q$ 作 $QM\perp y$ 轴于点 $M$，过 $E$ 点作 $x$ 轴的垂线交 $QM$ 于点 $N$．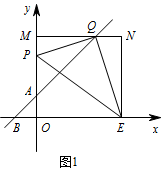
设点 $Q$ 的坐标为 $\left(x,x+2\right)$，
所以 $MQ=x$，$QN=10-x$ $,EN=x+2$，
在 $\mathrm {Rt}\triangle QEN$ 中，有 $QE^2=QN^2+EN^2$，即 $10^2=\left(10-x\right)^2+\left(x+2\right)^2$，解得 $x=4\pm\sqrt{14}$，
当 $x=4+\sqrt{14}$ 时，如图1，$y=x+2=6+\sqrt{14}$，所以点 $Q\left(4+\sqrt{14},6+\sqrt{14}\right)$，
当 $x=4-\sqrt{14}$ 时．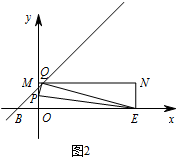
如图2，$y=x+2=6-\sqrt{14}$，所以点 $Q\left(4-\sqrt{14},6-\sqrt{14}\right)$，
综上所述，存在点 $Q$ 使以 $P,Q,E$ 三点为顶点的三角形与 $\triangle POE$ 全等，点 $Q$ 的坐标为存在，点 $Q$ 的坐标为 $\left(6,2\sqrt{21}\right)$，$\left(6,3\right)$，$\left(10,12\right)$，$\left(4+\sqrt{14},6+\sqrt{14}\right)$ 或 $\left(4-\sqrt{14},6-\sqrt{14}\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
