如图,在平面直角坐标系 $xOy$ 中,二次函数 $y=ax^2+bx-4$($a\neq 0$)的图象与 $x$ 轴交于 $A\left(-2,0\right)$,$C\left(8,0\right)$ 两点,与 $y$ 轴交于点 $B$,其对称轴与 $x$ 轴交于点 $D$.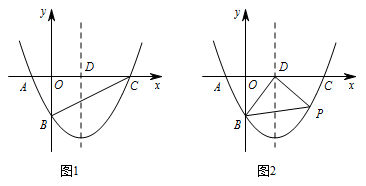

【难度】
【出处】
无
【标注】
-
如图 1,连接 $BC$,在线段 $BC$ 上是否存在点 $E$,使得 $\triangle CDE$ 为等腰三角形?若存在,求出所有符合条件的点 $E$ 的坐标;若不存在,请说明理由;标注答案存在,点 $E$ 的坐标为 $\left(8-2\sqrt5 ,- \sqrt5\right)$,$\left(0,-4\right)$,$\left(\dfrac{11}{2} ,-\dfrac54 \right)$解析因为二次函数 $y=ax^2+bx-4$ 的图象与 $x$ 轴交于 $A\left(-2,0\right),C\left(8,0\right)$ 两点,
所以 $\begin{cases}4a-2b-4=0,\\64a+8b-4=0,\end{cases}$ 解得 $\begin{cases}a=\dfrac14,\\b=-\dfrac32,\end{cases}$
所以该二次函数的解析式为 $y= \dfrac14x^2-\dfrac32 x-4$,
所以点 $B\left(0,-4\right)$.
设直线 $BC$ 的解析式为 $y=kx+b$.
所以 $\begin{cases}8k+b=0,\\b=-4.\end{cases}$ 解得 $\begin{cases}k=\dfrac12,\\b=-4,\end{cases}$
所以直线 $BC$ 的解析式为 $y=\dfrac12 x-4$.
设点 $E\left(m, \dfrac12m-4\right)$,则 $CE^2=\left(m-8\right)^2+\left( \dfrac12m-4\right)^2$.
由题意可得对称轴为 $x=3$,从而点 $D\left(3,0\right)$.
所以 $CD=5$,$CD^2=25$.
① 当 $CD=CE$ 时,有 $\left(m-8\right)^2+\left(\dfrac12 m-4\right)^2=5^2$.
解得 $m_1=8-2\sqrt5$,$m_2=8+2 \sqrt5$(舍去).
此时点 $E\left(8-2\sqrt5 ,-\sqrt5 \right)$;
② 当 $DC=DE$ 时,有 $\left(m-3\right)^2+\left(\dfrac12 m-4\right)^2=5^2$.
解得 $m_1=0$,$m_2=8$(舍去),
此时点 $E\left(0,-4\right)$;
③ 当 $EC=DE$ 时,有 $\left(m-8\right)^2+\left( \dfrac12m-4\right)^2=\left(m-3\right)^2+\left(\dfrac12 m-4\right)^2$.
解得 $m=5.5$.
此时点 $E\left(\dfrac{11}{2} ,-\dfrac54 \right)$.
综上所述,存在点 $E$,使得 $\triangle CDE$ 为等腰三角形,所有符合条件的点 $E$ 的坐标为 $\left(8-2\sqrt5 ,- \sqrt5\right)$,$\left(0,-4\right)$,$\left(\dfrac{11}{2} ,-\dfrac54 \right)$. -
如图 2,若点 $P\left(m,n\right)$ 是该二次函数图象上的一个动点(其中 $m>0$,$n<0$),连接 $PB,PD,BD$,求 $\triangle BDP$ 面积的最大值及此时点 $P$ 的坐标.标注答案$\triangle PBD$ 的最大面积为 $\dfrac{289}{24}$,点 $P$ 的坐标为 $\left(\dfrac{17}{3},-\dfrac{161}{36}\right)$解析由第1问可得 $n=\dfrac14m^2- \dfrac32m-4$.
过点 $P$ 作 $y$ 轴的平行线交 $x$ 轴于点 $F$. $\begin{split}\text{所以}S_{ \triangle PBD } &=S_{\text{梯形}OBPF}-S_{\triangle BOD}-S_{\triangle PFD}
$\begin{split}\text{所以}S_{ \triangle PBD } &=S_{\text{梯形}OBPF}-S_{\triangle BOD}-S_{\triangle PFD}
\\&=\dfrac12 m\left[4-\left(\dfrac14 m^2- \dfrac32m-4\right)\right]-\dfrac12 \left(m-3\right)\left[-\left(\dfrac14 m^2-\dfrac32 m-4\right)\right]- \dfrac12×3×4
\\&=- \dfrac38m^2+\dfrac{17}{4} m
\\&=-\dfrac38 \left(m-\dfrac{17}{3} \right)^2+\dfrac{289}{24}. \end{split}$
所以当 $m=\dfrac{17}{3} $ 时,$\triangle PBD$ 的最大面积为 $\dfrac{289}{24}$,
所以点 $P$ 的坐标为 $\left( \dfrac{17}{3},- \dfrac{161}{36}\right)$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2