已知抛物线 $y=x^2-2mx+m^2+m-1$（$m$ 是常数）的顶点为 $P$，直线 $l:y=x-1$．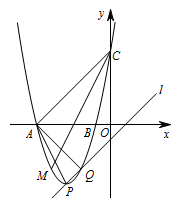
【难度】
【出处】
无
【标注】
-
当 $m=-3$ 时，抛物线与 $x$ 轴交于 $A,B$ 两点，与 $y$ 轴交于点 $C$，与直线 $l$ 的另一个交点为 $Q$，$M$ 是 $x$ 轴下方抛物线上的一点，$\angle ACM=\angle PAQ$（如图），求点 $M$ 的坐标；标注答案点 $M$ 的坐标为 $\left(-4,-3\right)$解析当 $m=-3$ 时，抛物线解析式为
$y=x^2+6x+5=(x+3)^2-4=(x+1)(x+5)$，
所以点 $A\left(-5,0\right)$，点 $B(-1,0)$，点 $C\left(0,5\right)$，点 $P\left(-3,-4\right)$．
联立方程组 $\begin{cases}y=x-1,\\ y=x^2+6x+5,\end{cases}$
解得 $\begin{cases}x_1=-3,\\ y_1=-4,\end{cases}\begin{cases}x_2=-2,\\ y_2=-3.\end{cases}$
所以点 $Q$ 的坐标为 $\left(-2,-3\right)$．
作 $ME\perp y$ 轴，$PF\perp x$ 轴，$QG\perp x$ 轴，垂足分别为点 $E,F,G$．
易得 $\angle CAO=\angle ACO=\angle OAQ=45^\circ$．
因为 $\angle APF=90^\circ-\left(\angle PAQ+45^\circ\right)=45^\circ-\angle PAQ$，
$\angle MCE=45^\circ-\angle ACM$，
而 $\angle ACM=\angle PAQ$，所以 $\angle APF=\angle MCE$．
所以 $\mathrm {Rt}\triangle CME\backsim \mathrm {Rt}\triangle PAF$．
从而 $\dfrac{CE}{PF}=\dfrac{ME}{AF}$．
设点 $M$ 的坐标为 $\left(x,x^2+6x+5\right)$，
则 $ME=-x$，$CE=-x^2-6x$，$PF=4$，$AF=2$．
所以 $\dfrac{-x^2-6x}{4}=\dfrac{-x}2$，
解得 $x_1=-4$，$x_2=0$（舍去）．
故点 $M$ 的坐标为 $\left(-4,-3\right)$． -
若以抛物线和直线 $l$ 的两个交点及坐标原点为顶点的三角形是等腰三角形，请直接写出所有符合条件的 $m$ 的值．标注答案$m$ 的值为 $0,\dfrac{1+\sqrt 3}2,\dfrac{1-\sqrt 3}2,\dfrac{-1+\sqrt 3}2$ 或 $\dfrac{-1-\sqrt 3}2$解析联立方程组 $\begin{cases}y=x-1,\\y=x^2-2mx+m^2+m-1,\end{cases}$
解得 $\begin{cases}x_1=m,\\y_1=m-1\end{cases},\begin{cases}x_2=m+1,\\y_2=m.\end{cases}$
所以点 $P$ 的坐标为 $\left(m,m-1\right)$，点 $Q$ 的坐标为 $\left(m+1,m\right)$．
$\therefore PQ^2=2$，$OP^2=2m^2-2m+1$，$OQ^2=2m^2+2m+1$．
分别令 $OP=OQ$，$OP=PQ$，$PQ=OQ$，
解得 $ m=0,\dfrac{1+\sqrt 3}2,\dfrac{1-\sqrt 3}2,\dfrac{-1+\sqrt 3}2$ 或 $\dfrac{-1-\sqrt 3}2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
