如图，在平面直角坐标系 $xOy$ 中，$\triangle ABO$ 为等腰直角三角形，$\angle ABO=90^\circ$，点 $A$ 的坐标为 $(4,0)$，点 $B$ 在第一象限．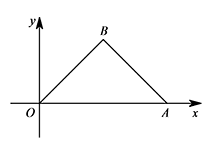
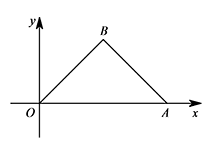
【难度】
【出处】
无
【标注】
-
若 $C$ 是 $BO$ 的中点，点 $Q$ 在线段 $AB$ 上，设点 $B$ 关于直线 $CQ$ 的对称点为 $B'$，当 $\triangle OCB'$ 为等边三角形时，求 $BQ$ 的长度；标注答案$BQ=\sqrt 6$解析由题意可得 $OA=4$，所以 $OB=AB=2\sqrt 2$．
如图，由轴对称的性质可得 $CB'=CB=CO$，$\angle B'CO=\angle BCO$．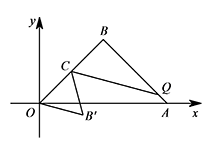
若 $\triangle OCB'$ 为等边三角形，则 $\angle B'CO=60^\circ$，
所以 $\angle B'CO=\angle BCO=60^\circ$．
从而在 $\mathrm{Rt}\triangle CBQ$ 中，$BQ=\sqrt 3 BC=\sqrt 6$． -
若点 $D$ 在线段 $BO$ 上，$OD=2DB$，点 $E,F$ 在 $\triangle OAB$ 的边上，且满足 $\triangle DOF$ 与 $\triangle DEF$ 全等，求点 $E$ 的坐标．标注答案满足条件的点 $E$ 的坐标为 $\left(\dfrac 83,0\right)$，$\left(2+\dfrac{2\sqrt 3}3,2-\dfrac{2\sqrt 3}3\right)$，$\left(\dfrac 83,\dfrac 43\right)$ 或 $(4,0)$解析由题意可得 $OD=\dfrac 23OB=\dfrac{4\sqrt 2}3$，$BD=\dfrac 13OB=\dfrac{2\sqrt 2}3$．
① 当点 $F$ 在 $OA$ 上时，
i）若 $\triangle DFO\cong \triangle DFE$，点 $E$ 在 $OA$ 上，如图所示．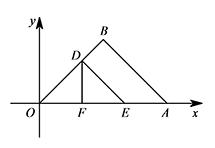
此时 $DF\perp OA$，所以 $OF=\dfrac{\sqrt{2}}2OD=\dfrac 43$．
所以 $OE=2OF=\dfrac 83$，即点 $E$ 的坐标为 $\left(\dfrac 83,0\right)$；
ii）若 $\triangle DFO\cong \triangle DFE$，点 $E$ 在 $AB$ 上，如图所示．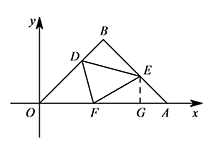
此时 $ED=OD=2BD$，所以 $\sin \angle BED=\dfrac{BD}{ED}=\dfrac 12$，
所以 $\angle BED=30^\circ$，
从而 $BE=\sqrt 3BD=\dfrac{2\sqrt 6}3$，$AE=\dfrac{6\sqrt 2-2\sqrt 6}3$．
过点 $E$ 作 $EG\perp OA$ 于点 $G$，则 $EG=AG=\dfrac{\sqrt 2}2AE=2-\dfrac{2\sqrt 3}3$，
所以 $OG=2+\dfrac{2\sqrt 3}3$，即点 $E$ 的坐标为 $\left(2+\dfrac{2\sqrt 3}3,2-\dfrac{2\sqrt 3}3\right)$；
iii）若 $\triangle DFO\cong \triangle FDE$，点 $E$ 在 $AB$ 上，如图所示．
此时 $DE\parallel OA$，所以 $BD=BE$，
从而 $AE=OD=\dfrac{4\sqrt 2}3$．
过点 $E$ 作 $EG\perp OA$ 于点 $G$，则 $EG=AG=\dfrac{\sqrt 2}2AE=\dfrac 43$，
所以 $OG=\dfrac 83$，即点 $E$ 的坐标为 $\left(\dfrac 83,\dfrac 43\right)$；
② 当点 $F$ 在 $AB$ 上时，只能有 $\triangle ODF\cong \triangle AFD$，如图所示．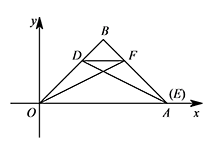
此时点 $DF\parallel OA$，且点 $E$ 与点 $A$ 重合，
即点 $E$ 的坐标为 $(4,0)$．
综上可得，满足条件的点 $E$ 的坐标为 $\left(\dfrac 83,0\right)$，$\left(2+\dfrac{2\sqrt 3}3,2-\dfrac{2\sqrt 3}3\right)$，$\left(\dfrac 83,\dfrac 43\right)$ 或 $(4,0)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
