一次函数 $y=\dfrac 34x$ 的图象如图所示，它与二次函数 $y=ax^2-4ax+c$ 的图象交于 $A,B$ 两点（其中点 $A$ 在点 $B$ 的左侧），与这个二次函数图象的对称轴交于点 $C$．设二次函数图象的顶点为 $D$．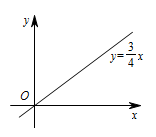
【难度】
【出处】
无
【标注】
-
若点 $D$ 与点 $C$ 关于 $x$ 轴对称，且 $\triangle ACD$ 的面积等于 $3$，求此二次函数的关系式；标注答案二次函数的解析式为 $y=\dfrac 38x^2-\dfrac 32x$解析由 $y=ax^2-4ax+c=a\left(x-2\right)^2-4a+c$，
可得二次函数图象的对称轴为直线 $x=2$．
把 $x=2$ 代入一次函数 $y=\dfrac 34x$ 解析式，得点 $C\left(2,\dfrac 32\right)$．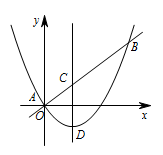
因为点 $D$ 与点 $C$ 关于 $x$ 轴对称，
从而点 $D\left(2,-\dfrac 32\right)$，$CD=3$．
设 $A\left(m,\dfrac 34 m\right)$，则 $m<2$．
由 $S_{\triangle ACD}=3$，得 $\dfrac 12\times 3\times \left(2-m\right)=3$，
解得 $m=0$，即点 $A\left(0,0\right)$．
将 $A,D$ 坐标代入二次函数解析式，得 $\begin{cases} c=0, \\ -4a+c=-\dfrac 32,\end{cases}$
解得 $\begin{cases}a=\dfrac 38,\\c=0.\end{cases}$
所以二次函数的解析式为 $y=\dfrac 38x^2-\dfrac 32x$． -
若 $CD=AC$，且 $\triangle ACD$ 的面积等于 $10$，求此二次函数的关系式．标注答案二次函数的解析式为 $y=\dfrac 18x^2-\dfrac 12x-3$ 或 $y=-\dfrac 12x^2+2x+\dfrac 92$解析过点 $A$ 作 $AE\perp CD$ 于点 $E$．
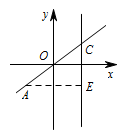设 $A\left(m,\dfrac 34m\right)$，则 $m<2$．则 $AE=2-m$，$CE=\dfrac 32-\dfrac 34m$，
从而 $AC=\sqrt {AE^2+CE^2}=\sqrt {\left(2-m\right)^2+\left(\dfrac 32-\dfrac 34m\right)^2} =\dfrac 54\left(2-m\right)$．
由 $S_{\triangle ACD}=10$，得 $\dfrac 12\times \dfrac 54\left(2-m\right)^2=10$，
解得 $m_1=-2$，$m_2=6$（舍去），
所以点 $A\left(-2,-\dfrac 32\right)$，$CD=5$．
① 若 $a>0$，则点 $D$ 在点 $C$ 下方，则点 $D\left(2,-\dfrac 72\right)$．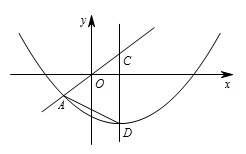
所以 $\begin{cases} 12a+c=-\dfrac 32,\\ -4a+c=-\dfrac 72,\end{cases}$ 解得 $\begin{cases} a=\dfrac 18, \\ c=-3.\end{cases}$
此时二次函数解析式为 $y=\dfrac 18x^2-\dfrac 12x-3$；
② 若 $a<0$，则点 $D$ 在点 $C$ 上方，则点 $D\left(2,\dfrac {13}{2}\right)$．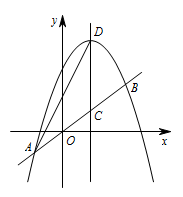
所以 $\begin{cases}12a+c=-\dfrac 32, \\ -4a+c=\dfrac {13}{2}.\end{cases}$ 解得 $\begin{cases}a=-\dfrac 12, \\ c=\dfrac 92.\end{cases}$
此时二次函数的解析式为 $y=-\dfrac 12x^2+2x+\dfrac 92$．
综上可得，二次函数的解析式为 $y=\dfrac 18x^2-\dfrac 12x-3$ 或 $y=-\dfrac 12x^2+2x+\dfrac 92$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
