如图,在直角梯形 $ABCD$ 中,$AD\parallel BC$,$\angle B=90^\circ$,$AD=2$,$BC=6$,$AB=3$.$E$ 为 $BC$ 边上一点,当 $BE=2$ 时,以 $BE$ 为边作正方形 $BEFG$,使正方形 $BEFG$ 和梯形 $ABCD$ 在 $BC$ 的同侧.当正方形 $BEFG$ 沿 $BC$ 向右平移,记平移中的正方形 $BEFG$ 为正方形 $B'EFG$,当点 $E$ 与点 $C$ 重合时停止平移.设平移的距离为 $t$,正方形 $B'EFG$ 的边 $EF$ 与 $AC$ 交于点 $M$,连接 $B'D,B'M,DM$.是否存在这样的 $t$,使 $\triangle B'DM$ 是直角三角形?若存在,求出 $t$ 的值;若不存在,请说明理由.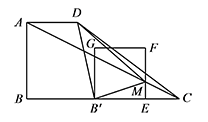
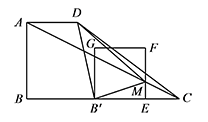
【难度】
【出处】
无
【标注】
【答案】
存在,当 $t={\dfrac{20}{7}}$ 或 $-3+{\sqrt{17}}$ 时,$\triangle B'DM$ 是直角三角形
【解析】
如图,过 $D$ 作 $DH\perp BC$ 于点 $H$,作 $MN\perp DH$ 于点 $N$. 则 $BH=AD=2$,$DH=AB=3$.
则 $BH=AD=2$,$DH=AB=3$.
所以 $BB'=HE=t$,$HB'=|t-2|$,$EC=4-t$.
易证 $\triangle MEC \sim \triangle ABC$,
可得 ${\dfrac{ME}{AB}}={\dfrac{EC}{BC}}$,即 ${\dfrac{ME}{3}}={\dfrac{4-t}{6}}$,
所以 $ME=2-{\dfrac{1}{2}}t$.
在 ${\mathrm{Rt}}\triangle B'ME$ 中,有 $B'M^2=ME^2+B'E^2={\dfrac{1}{4}}t^2-2t+8$.
在 ${\mathrm{Rt}}\triangle DHB'$ 中,有 $B'D^2=DH^2+B'H^2=t^2-4t+13$.
在 ${\mathrm{Rt}}\triangle DMN$ 中,$DN=DH-NH={\dfrac{1}{2}}t+1$,则 $DM^2=DN^2+MN^2={\dfrac{5}{4}}t^2+t+1$.
① 若 $\angle DB'M=90^\circ$,则 $DM^2=B'M^2+B'D^2$,
即 ${\dfrac{5}{4}}t^2+t+1=\left({\dfrac{1}{4}}t^2-2t+8 \right)+\left(t^2-4t+13\right)$,
解得 $t={\dfrac{20}{7}}$;
② 若 $\angle B'MD=90^\circ$,则 $B'D^2=B'M^2+MD^2$,
即 $t^2-4t+13= \left({\dfrac{1}{4}}t^2-2t+8 \right)+ \left({\dfrac{5}{4}}t^2+t+1\right)$,
解得 $t_1=-3+{\sqrt{17}}$,$t_2=-3-{\sqrt{17}}$(舍去);
③ 若 $\angle B'DM=90^\circ$,则 $B'M^2=B'D^2+MD^2$,
即 ${\dfrac{1}{4}}t^2-2t+8=\left(t^2-4t+13\right)+\left({\dfrac{5}{4}}t^2+t+1\right)$,
此方程无解.
综上所得,当 $t={\dfrac{20}{7}}$ 或 $-3+{\sqrt{17}}$ 时,$\triangle B'DM$ 是直角三角形.
 则 $BH=AD=2$,$DH=AB=3$.
则 $BH=AD=2$,$DH=AB=3$.所以 $BB'=HE=t$,$HB'=|t-2|$,$EC=4-t$.
易证 $\triangle MEC \sim \triangle ABC$,
可得 ${\dfrac{ME}{AB}}={\dfrac{EC}{BC}}$,即 ${\dfrac{ME}{3}}={\dfrac{4-t}{6}}$,
所以 $ME=2-{\dfrac{1}{2}}t$.
在 ${\mathrm{Rt}}\triangle B'ME$ 中,有 $B'M^2=ME^2+B'E^2={\dfrac{1}{4}}t^2-2t+8$.
在 ${\mathrm{Rt}}\triangle DHB'$ 中,有 $B'D^2=DH^2+B'H^2=t^2-4t+13$.
在 ${\mathrm{Rt}}\triangle DMN$ 中,$DN=DH-NH={\dfrac{1}{2}}t+1$,则 $DM^2=DN^2+MN^2={\dfrac{5}{4}}t^2+t+1$.
① 若 $\angle DB'M=90^\circ$,则 $DM^2=B'M^2+B'D^2$,
即 ${\dfrac{5}{4}}t^2+t+1=\left({\dfrac{1}{4}}t^2-2t+8 \right)+\left(t^2-4t+13\right)$,
解得 $t={\dfrac{20}{7}}$;
② 若 $\angle B'MD=90^\circ$,则 $B'D^2=B'M^2+MD^2$,
即 $t^2-4t+13= \left({\dfrac{1}{4}}t^2-2t+8 \right)+ \left({\dfrac{5}{4}}t^2+t+1\right)$,
解得 $t_1=-3+{\sqrt{17}}$,$t_2=-3-{\sqrt{17}}$(舍去);
③ 若 $\angle B'DM=90^\circ$,则 $B'M^2=B'D^2+MD^2$,
即 ${\dfrac{1}{4}}t^2-2t+8=\left(t^2-4t+13\right)+\left({\dfrac{5}{4}}t^2+t+1\right)$,
此方程无解.
综上所得,当 $t={\dfrac{20}{7}}$ 或 $-3+{\sqrt{17}}$ 时,$\triangle B'DM$ 是直角三角形.
答案
解析
备注