查看数据源：5911218ce020e7000a79879d
已知函数 $f(x)=x^2-2(a+2)x+a^2$，$g(x)=-x^2+2(a-2)x-a^2+8$，设 $H_1(x)=\max\left\{f(x),g(x)\right\}$，$H_2(x)=\min\left\{f(x),g(x)\right\}$．记 $H_1(x)$ 的最小值为 $A$，$H_2(x)$ 的最大值为 $B$，则 $A-B=$  \((\qquad)\)
A: $a^2-2a-16$
B: $a^2+2a-16$
C: $-16$
D: $16$
【难度】
【出处】
2013年高考辽宁卷（文）
【标注】
  • 知识点
    >
    函数
    >
    常见初等函数
    >
    二次函数
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的最值和值域
【答案】
C
【解析】
要考虑 $f(x),g(x)$ 的大小，作差$$f(x)-g(x)=2(x^2-2ax+a^2-4),$$记 $h(x)=x^2-2ax+a^2-4$，则 $h(x)$ 一定有两个零点$$x_1=a-2,x_2=a+2,$$对应的点 $M(x_1,f(x_1)),N(x_2,f(x_2))$ 为 $f(x),g(x)$ 的交点，且 $M$ 点恰为 $g(x)$ 的顶点，$N$ 点恰为 $f(x)$ 的顶点，示意图如下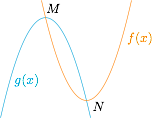：结合示意图知$$A=N_y=f(x_2),B=M_y=f(x_1).$$于是$$ A-B=f(x_2)-f(x_1)=(x_2-x_1)[x_2+x_1-2(a+2)]=-16.$$
题目 答案 解析 备注
0.109532s