如图，在平面直角坐标系 $xOy$ 中，$\mathrm{Rt}\triangle OAB$ 的直角顶点 $A$ 在 $x$ 轴上，$OA=4$，$AB=3$．动点 $M$ 从点 $A$ 出发，以每秒 $1$ 个单位长度的速度，沿 $AO$ 向终点 $O$ 移动；同时点 $N$ 从点 $O$ 出发，以每秒 $1.25$ 个单位长度的速度，沿 $OB$ 向终点 $B$ 移动．当两个动点运动了 $x$ 秒（$0<x<4$）时，解答下列问题：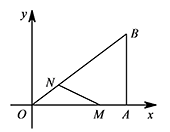
【难度】
【出处】
无
【标注】
-
求点 $N$ 的坐标（用含 $x$ 的代数式表示）；标注答案点 $N$ 的坐标为 $\left(x,\dfrac 34x\right)$解析在 $\mathrm{Rt}\triangle OAB$ 中，由勾股定理得 $OB=\sqrt{OA^2+AB^2}=5$．
如图，过点 $N$ 作 $NP\perp OA$ 于点 $P$．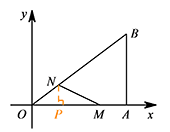
易证 $\triangle PON\sim \triangle AOB$，
从而 $\dfrac{OP}{OA}=\dfrac{ON}{OB}=\dfrac{PN}{AB}$，
所以 $OP=x$，$PN=\dfrac 34x$．
即点 $N$ 的坐标为 $\left(x,\dfrac 34x\right)$． -
在两个动点运动过程中，是否存在某一时刻，使 $\triangle OMN$ 是直角三角形？若存在，求出 $x$ 的值；若不存在，请说明理由．标注答案存在，$\triangle OMN$ 是直角三角形时 $x$ 的值为 $2$ 或 $\dfrac{64}{41}$解析当 $\triangle OMN$ 是直角三角形时，可得 $\triangle OMN$ 和 $\triangle OAB$ 相似．分两种情况：
① 若 $\angle MNO=90^\circ$，则有 $\dfrac{OM}{OB}=\dfrac{ON}{OA}$，
即 $\dfrac{4-x}{5}=\dfrac{1.25x}{4}$，
解得 $x=\dfrac{64}{41}$；
② 若 $\angle OMN=90^\circ$，则有 $\dfrac{OM}{OA}=\dfrac{ON}{OB}$，
即 $\dfrac{4-x}{4}=\dfrac{1.25x}{5}$，
解得 $x=2$．
综上可得，$\triangle OMN$ 是直角三角形时 $x$ 的值为 $2$ 或 $\dfrac{64}{41}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
