查看数据源：5912a95ee020e70007fbedf8
如图，在矩形 $ABCO$ 中，点 $O$ 为坐标原点，点 $B$ 的坐标为 $\left(4,3\right)$，点 $A$，$C$ 在坐标轴上，点 $P$ 在 $BC$ 边上，直线 $l$：$y =2 x-3$．已知点 $M$ 在第一象限，且是直线 $l$ 上的点，若 $\triangle APM$ 是等腰直角三角形，求点 $M$ 的坐标．
【难度】
【出处】
无
【标注】
  • 题型
    >
    代几综合
    >
    直角三角形的存在性
【答案】
点 $M$ 的坐标可以为 $\left(\dfrac{14}{3},\dfrac{19}{3}\right)$，$\left(2,1\right)$，$\left(\dfrac{10}{3},\dfrac{11}{3}\right)$
【解析】
① 若点 $A$ 为直角顶点时，点 $M$ 在第一象限，连接 $AC$，如图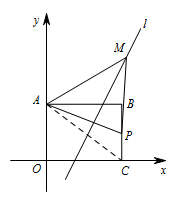．因为 $\angle APB>\angle ACB>45^{\circ}$，
所以 $\triangle APM$ 不可能为等腰直角三角形，
所以此时点 $M$ 不存在．
② 若点 $P$ 为直角顶点时，点 $M$ 在第一象限，如图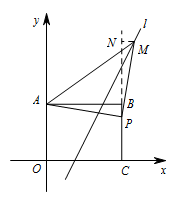．过点 $M$ 作 $MN\perp CB$，交 $CB$ 的延长线于点 $N$，
则 $\mathrm {Rt}\triangle ABP\cong \mathrm {Rt}\triangle PNM$，
所以 $AB=PN=4$，$MN=BP$．
设点 $M\left(x,2x-3\right)$，则 $MN=x-4$．
所以 $2x-3=4+3-\left(x-4\right)$．
所以 $x=\dfrac{14}{3}$．
所以此时点 $M\left(\dfrac{14}{3},\dfrac{19}{3}\right)$．
③ 若点 $M$ 为直角顶点，点 $M$ 在第一象限，如图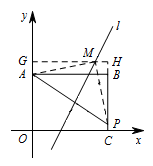．过点 $M$ 作 $MG\perp OA$ 于点 $G$，交 $BC$ 于点 $H$．
则 $\mathrm {Rt}\triangle AGM\cong \mathrm {Rt}\triangle MHP$．
所以 $AG=MH$．
设点 $M\left(x,2x-3\right)$，则 $AG=|2x-6|$，$MH=|4-x|$．
所以 $|2x-6|=|4-x|$，
解得 $x_1=2$，$x_2=\dfrac{10}3$．
所以 $x+3-\left(2x-3\right)=4$．
所以 $x=2$．
所以此时点 $M_1\left(2,1\right)$，点 $M_2\left(\dfrac{10}{3},\dfrac{11}{3}\right)$．
综上所述，点 $M$ 的坐标可以为 $\left(\dfrac{14}{3},\dfrac{19}{3}\right)$，$\left(2,1\right)$，$\left(\dfrac{10}{3},\dfrac{11}{3}\right)$．
答案 解析 备注
0.171850s